Question

【题目】如图,点A(a,2)、B(2,b)都在双曲线(x<0)上,点P、Q分别是x轴、y轴上的动点,当四边形PABQ的周长取最小值时,PQ所在直线的解析式是，则k的值为（ ）

A.-7B.-4C.3D.7

Answer 1

【答案】A

【解析】

作A点关于x轴的对称点C，B点关于y轴的对称点D，根据对称的性质得到C点、D点坐标．CD分别交x轴、y轴于P点、Q点，根据两点之间线段最短得此时四边形PABQ的周长最小，然后利用一次函数图象上点的坐标特征来求k的值．

作A点关于x轴的对称点C,B点关于y轴的对称点D,所以C点坐标为(a,2),D点坐标为(2,b)，

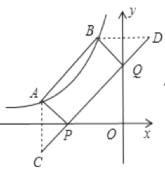
连结CD分别交x轴、y轴于P点、Q点，此时四边形PABQ的周长最小，

把C点的坐标代入y=x+1.5得到：2=a+1.5，

解得a= ，

则k=2a=7.

故选A.