题目内容
已知一次函数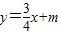 的图象分别交x轴、y轴于A、B两点(如图),且与反比例函数
的图象分别交x轴、y轴于A、B两点(如图),且与反比例函数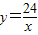 的图象在第一象限交于点C(4,n),CD⊥x轴于D.
的图象在第一象限交于点C(4,n),CD⊥x轴于D.(1)求m、n的值;
(2)如果点P在x轴上,并在点A与点D之间,点Q在线段AC上,且AP=CQ,那么当△APQ与△ADC相似时,求点Q的坐标.

【答案】分析:(1)把C点坐标代入反比例函数解析式求出n,得C点坐标,再代入一次函数解析式求m;
(2)根据△APQ∽△ADC,然后相似比求解.
解答: 解:(1)∵点C(4,n)在
解:(1)∵点C(4,n)在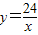 的图象上,
的图象上,
∴n=6,
∴C(4,6)(1分)
∵点C(4,6)在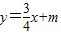 的图象上,
的图象上,
∴m=3(1分)
(2)∵当x=0时,y=3;当y=0时,x=-4.所以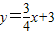 与x轴交于点A(-4,0),与y轴交于点B(0,3)(2分)
与x轴交于点A(-4,0),与y轴交于点B(0,3)(2分)
设AP=CQ=t,
∵C(4,6),CD⊥x轴,
∴AD=8,CD=6,
∴AC=10,
∴AQ=10-t,
∵△APQ与△ADC相似,且∠A=∠A,
∴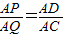 或
或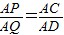 ,即
,即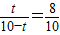 或
或 (2分)
(2分)
∴ 或
或 (2分)
(2分)
∵点Q在直线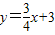 上,
上,
∴设 (-4<t<4)(1分)
(-4<t<4)(1分)
作QH⊥x轴,则AH=x+4
∵QH∥CD,
∴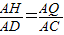 ,即
,即 (1分)
(1分)
当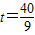 时,
时,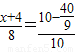 ,解得:
,解得: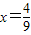 ,
,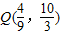 (1分)
(1分)
当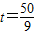 时,
时,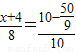 ,解得:
,解得: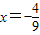 ,
, (1分).
(1分).
综上所述,Q点的坐标为Q( ,
,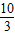 )、(-
)、(- ,
, ).
).
点评:此题的相似没有注明对应关系,所以必须分类讨论.分类讨论检查学生思维的严密性.
(2)根据△APQ∽△ADC,然后相似比求解.
解答:
 解:(1)∵点C(4,n)在
解:(1)∵点C(4,n)在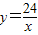 的图象上,
的图象上,∴n=6,
∴C(4,6)(1分)
∵点C(4,6)在
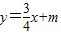 的图象上,
的图象上,∴m=3(1分)
(2)∵当x=0时,y=3;当y=0时,x=-4.所以
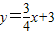 与x轴交于点A(-4,0),与y轴交于点B(0,3)(2分)
与x轴交于点A(-4,0),与y轴交于点B(0,3)(2分)设AP=CQ=t,
∵C(4,6),CD⊥x轴,
∴AD=8,CD=6,
∴AC=10,
∴AQ=10-t,
∵△APQ与△ADC相似,且∠A=∠A,
∴
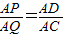 或
或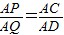 ,即
,即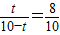 或
或 (2分)
(2分)∴
 或
或 (2分)
(2分)∵点Q在直线
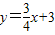 上,
上,∴设
 (-4<t<4)(1分)
(-4<t<4)(1分)作QH⊥x轴,则AH=x+4
∵QH∥CD,
∴
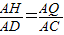 ,即
,即 (1分)
(1分)当
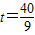 时,
时,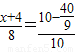 ,解得:
,解得: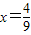 ,
,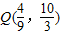 (1分)
(1分)当
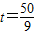 时,
时,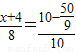 ,解得:
,解得: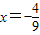 ,
, (1分).
(1分).综上所述,Q点的坐标为Q(
 ,
,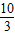 )、(-
)、(- ,
, ).
).点评:此题的相似没有注明对应关系,所以必须分类讨论.分类讨论检查学生思维的严密性.

练习册系列答案
相关题目
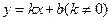 的图象与x轴、y轴分别交于A、B两点,且与反比例函数
的图象与x轴、y轴分别交于A、B两点,且与反比例函数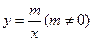 的图象在第一象限交于C点,CD垂直与x轴,垂足为D.若OA=OB=OD=1,
的图象在第一象限交于C点,CD垂直与x轴,垂足为D.若OA=OB=OD=1,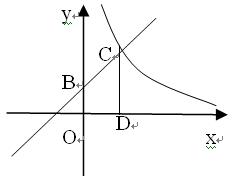
 的图象与x轴、y轴分别交于A、B两点,且与反比例函数
的图象与x轴、y轴分别交于A、B两点,且与反比例函数 的图象在第一象限交于C点,CD垂直与x轴,垂足为D.若OA=OB=OD=1,
的图象在第一象限交于C点,CD垂直与x轴,垂足为D.若OA=OB=OD=1,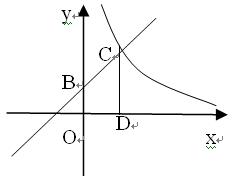
 的图象经过点
的图象经过点 ,且与函数
,且与函数 的图象相交于点
的图象相交于点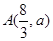 .
. 的值;(2分)
的值;(2分) 轴的交点是B,函数
轴的交点是B,函数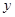 轴的交点是C,求四边形
轴的交点是C,求四边形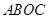 的面积(其中O为坐标原点).(4分)
的面积(其中O为坐标原点).(4分)