题目内容
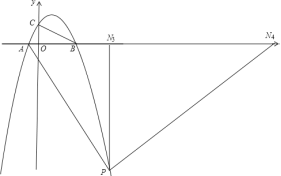
【题目】如图,抛物线y=![]() 交x轴于点A、B,交y轴于点C,点A的坐标是(-1,0),点C的坐标是(0,2).
交x轴于点A、B,交y轴于点C,点A的坐标是(-1,0),点C的坐标是(0,2).
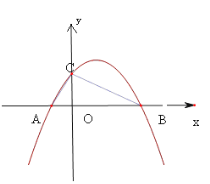
(1)求该抛物线的解析式。
(2)已知点P是抛物线上的一个动点,点N在x轴上。
①若点P在x轴上方,且△APN是等腰直角三角形,求点N的坐标;
②若点P在x轴下方,且△APN∽△BOC,请直接写出点N的坐标。
【答案】(1)y=![]() ;
;
(2)①点N的坐标是(2,0)或(5,0);
②N的坐标为(5,0)或(6.5,0)或(8,0)或(44,0).
【解析】
试题分析:(1)把A、C两点的坐标代入函数解析式,即可得到关于b,c的方程组,从而求得b,c的值,求得函数的解析式;
(2)①首先由点P、A、B都在抛物线上,且A、B在x轴上,得出点A不可能是直角顶点,那么当△APN是等腰直角三角形时,∠PAN=45°.作∠BAP=45°,AP交抛物线于点P,设点P坐标是(t,![]() ).再分两种情况进行讨论:(Ⅰ)当点N是直角顶点时,过点P作
).再分两种情况进行讨论:(Ⅰ)当点N是直角顶点时,过点P作![]() ⊥x轴于点
⊥x轴于点![]() ,则
,则![]() =
=![]() ,依此列出方程
,依此列出方程![]() =t+1,解方程求出N1的坐标;(Ⅱ)当点P是直角顶点时,过点P作
=t+1,解方程求出N1的坐标;(Ⅱ)当点P是直角顶点时,过点P作![]() ⊥AP,
⊥AP,![]() 交x轴于点
交x轴于点![]() ,则AP=
,则AP=![]() ,那么
,那么![]() =
=![]() =2-(-1)=3,则
=2-(-1)=3,则![]() =2+3=5,
=2+3=5,![]() 的坐标可求;②先由抛物线解析式求出B点坐标,根据△BOC是直角三角形,得出△ANP也是直角三角形,由A点不可能是直角顶点,得出直角顶点可能是P点或N点.设点P坐标是(t,
的坐标可求;②先由抛物线解析式求出B点坐标,根据△BOC是直角三角形,得出△ANP也是直角三角形,由A点不可能是直角顶点,得出直角顶点可能是P点或N点.设点P坐标是(t,![]() ),则
),则![]() t+2<0.再分两种情况进行讨论:(Ⅰ)过A作BC的平行线,交抛物线于点P,则∠PAB=∠OBC.过P作
t+2<0.再分两种情况进行讨论:(Ⅰ)过A作BC的平行线,交抛物线于点P,则∠PAB=∠OBC.过P作![]() ⊥x轴于点N1,则
⊥x轴于点N1,则![]() ∽△BOC,N1(t,0).由
∽△BOC,N1(t,0).由![]() ∽△BOC,根据相似三角形对应边成比例求出t的值,得出点N1的坐标;过点P作
∽△BOC,根据相似三角形对应边成比例求出t的值,得出点N1的坐标;过点P作![]() ⊥AP,
⊥AP,![]() 交x轴于点
交x轴于点![]() ,则
,则![]() ∽△BOC.由
∽△BOC.由![]() ∽△
∽△![]() ,根据相似三角形对应边成比例求出t的值,得出点
,根据相似三角形对应边成比例求出t的值,得出点![]() 的坐标;(Ⅱ)在x轴下方作∠BAP=∠OCB,交抛物线于点P,过P作
的坐标;(Ⅱ)在x轴下方作∠BAP=∠OCB,交抛物线于点P,过P作![]() ⊥x轴于点
⊥x轴于点![]() ,则
,则![]() ∽△COB,
∽△COB,![]() (t,0).由
(t,0).由![]() ∽△COB,根据相似三角形对应边成比例求出t的值,得出点
∽△COB,根据相似三角形对应边成比例求出t的值,得出点![]() 的坐标;过点P作
的坐标;过点P作![]() ⊥AP,
⊥AP,![]() 交x轴于点N4,则
交x轴于点N4,则![]() ∽△COB.由
∽△COB.由![]() ∽
∽![]() ,根据相似三角形对应边成比例求出t的值,得出点N4的坐标.
,根据相似三角形对应边成比例求出t的值,得出点N4的坐标.
试题解析:(1)∵抛物线y=![]() 过点A(-1,0),C(0,2),∴
过点A(-1,0),C(0,2),∴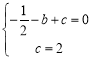 ,解得
,解得![]() ,∴该抛物线的解析式是:y=
,∴该抛物线的解析式是:y=![]() ;
;
(2)①∵点P、A、B都在抛物线上,且A、B在x轴上,∴点A不可能是直角顶点,则∠PAN=45°.如图,作∠BAP=45°,AP交抛物线于点P.设点P坐标是(t,![]() ).
).
(Ⅰ)过点P作![]() ⊥x轴于点
⊥x轴于点![]() ,则
,则![]() =
=![]() ,即-
,即-![]() =t+1,解得
=t+1,解得![]() =2,
=2,![]() =-1(不合题意舍去),所以
=-1(不合题意舍去),所以![]() 的坐标是(2,0);
的坐标是(2,0);
(Ⅱ)当点P是直角顶点时,过点P作![]() ⊥AP,
⊥AP,![]() 交x轴于点
交x轴于点![]() ,则AP=
,则AP=![]() ,
,![]() =
=![]() =2-(-1)=3,则
=2-(-1)=3,则![]() =2+3=5,所以
=2+3=5,所以![]() 的坐标是(5,0);综上所述,点N的坐标是(2,0)或(5,0);
的坐标是(5,0);综上所述,点N的坐标是(2,0)或(5,0);
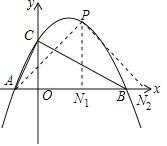
②∵y=![]() ,∴当y=0时,
,∴当y=0时,![]() =0,解得x=-1或4,∵A(-1,0),∴B(4,0),∴△BOC中,OB=4,OC=2,∠BOC=90°.∵△BOC是直角三角形,∴当△ANP与△BOC相似时,△ANP也是直角三角形,∵A点不可能是直角顶点,∴直角顶点可能是P点或N点.设点P坐标是(t,
=0,解得x=-1或4,∵A(-1,0),∴B(4,0),∴△BOC中,OB=4,OC=2,∠BOC=90°.∵△BOC是直角三角形,∴当△ANP与△BOC相似时,△ANP也是直角三角形,∵A点不可能是直角顶点,∴直角顶点可能是P点或N点.设点P坐标是(t,![]() ),则
),则![]() <0.
<0.
(Ⅰ)过A作BC的平行线,交抛物线于点P,则∠PAB=∠OBC.过P作![]() ⊥x轴于点
⊥x轴于点![]() ,则
,则![]() ∽△BOC,
∽△BOC,![]() (t,0).∵
(t,0).∵![]() ∽△BOC,∴
∽△BOC,∴![]() =
=![]() ,∴
,∴![]() =
=![]()
![]() ==2,∴AN1=2N1P,即t+1=2(
==2,∴AN1=2N1P,即t+1=2(![]() ),解得
),解得![]() =5,
=5,![]() =-1(不合题意舍去),所以点P的坐标是(5,-3),点
=-1(不合题意舍去),所以点P的坐标是(5,-3),点![]() 的坐标是(5,0);过点P作
的坐标是(5,0);过点P作![]() ⊥AP,
⊥AP,![]() 交x轴于点
交x轴于点![]() ,则
,则![]() ∽△BOC.∵
∽△BOC.∵![]() ∽
∽![]() ,∴
,∴![]() ,∴
,∴![]() =
=![]() =1.5,∴
=1.5,∴![]() =
=![]() =5+1.5=6.5,∴点
=5+1.5=6.5,∴点![]() 的坐标是(6.5,0);
的坐标是(6.5,0);
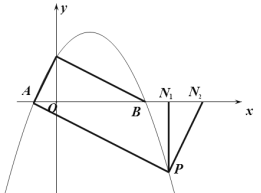
(Ⅱ)在x轴下方作∠BAP=∠OCB,交抛物线于点P,过P作![]() ⊥x轴于点
⊥x轴于点![]() ,则
,则![]() ∽△COB,
∽△COB,![]() (t,0).∵
(t,0).∵![]() ∽△COB,∴
∽△COB,∴![]() ,∴
,∴![]() =
=![]() ,∴
,∴![]() ,即
,即![]() =2(t+1),解得
=2(t+1),解得![]() =8,
=8,![]() =-1(不合题意舍去),所以点P的坐标是(8,-18),点
=-1(不合题意舍去),所以点P的坐标是(8,-18),点![]() 的坐标是(8,0);过点P作
的坐标是(8,0);过点P作![]() ⊥AP,
⊥AP,![]() 交x轴于点
交x轴于点![]() ,则
,则![]() ∽△COB.∵
∽△COB.∵![]() ∽
∽![]() ,∴
,∴![]() ,∴
,∴![]() =
=![]() =36,∴
=36,∴![]() =8+36=44,∴点
=8+36=44,∴点![]() 的坐标是(44,0);综上所述,所求点N的坐标为
的坐标是(44,0);综上所述,所求点N的坐标为![]() (5,0),
(5,0),![]() (6.5,0),
(6.5,0),![]() (8,0),
(8,0),![]() (44,0).
(44,0).