题目内容
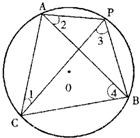 16、如图:A、B、C是⊙O上的三个定点,∠ACB=70°,P是⊙O上的动点,但不与A、B、C重合,那么下列说法正确的序号是
16、如图:A、B、C是⊙O上的三个定点,∠ACB=70°,P是⊙O上的动点,但不与A、B、C重合,那么下列说法正确的序号是①②④
(多填或错填得0分,少填酌情给分)①∠APB=110°或70°
②当P点在劣弧AB上时,图中∠1+∠2+∠3+∠4=180°
③以A、P、B、C为顶点的四边形不可能是平行四边形
④以A、P、B、C为顶点的四边形可以是等腰梯形.
分析:根据等弧所对的圆周角相等、圆内接四边形的对角互补的性质进行逐一分析.
解答:解:①当点P在劣弧上时,则∠APB=180°-∠ACB=110°;当点P在优弧上时,则∠APB=∠ACB=70°,故该选项正确;
②如图所示,则∠1=∠ABP,∠4=∠APC,则∠1+∠2+∠3+∠4=∠ABP+∠2+∠3+∠APC=180°,故该选项正确;
③圆内接平行四边形必是矩形,所以以A、P、B、C为顶点的四边形不可能是平行四边形,故该选项错误;
④只需保证AP∥BC,则以A、P、B、C为顶点的四边形可以是等腰梯形,故该选项正确.
故答案为①②④.
②如图所示,则∠1=∠ABP,∠4=∠APC,则∠1+∠2+∠3+∠4=∠ABP+∠2+∠3+∠APC=180°,故该选项正确;
③圆内接平行四边形必是矩形,所以以A、P、B、C为顶点的四边形不可能是平行四边形,故该选项错误;
④只需保证AP∥BC,则以A、P、B、C为顶点的四边形可以是等腰梯形,故该选项正确.
故答案为①②④.
点评:此题主要考查了圆周角定理的推论以及圆内接四边形的性质.注意:圆内接平行四边形必是矩形;圆内接梯形必是等腰梯形.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
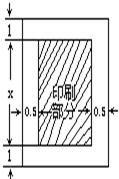 印刷一张矩形的张贴广告(如图),它的印刷面积是32dm2,上下空白各1dm,两边空白各0.5dm.当要求四周空白处的面积为18dm2时,求用来印刷这张广告的纸张的长和宽各是多少(图中长度的单位:dm).
印刷一张矩形的张贴广告(如图),它的印刷面积是32dm2,上下空白各1dm,两边空白各0.5dm.当要求四周空白处的面积为18dm2时,求用来印刷这张广告的纸张的长和宽各是多少(图中长度的单位:dm).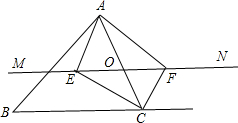 如图,△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA相邻的外角平分线CF于点F,点O运动到何处时,四边形AECF是矩形?
如图,△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA相邻的外角平分线CF于点F,点O运动到何处时,四边形AECF是矩形?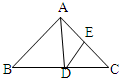 12、如图,在△ABC中,DE是AC的中垂线,AE=2.5cm,△ABD的周长是9cm,则△ABC的周长是
12、如图,在△ABC中,DE是AC的中垂线,AE=2.5cm,△ABD的周长是9cm,则△ABC的周长是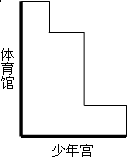 32、如图,粗线和细线是公交车从体育馆到少年宫的两条行驶路线.
32、如图,粗线和细线是公交车从体育馆到少年宫的两条行驶路线.