题目内容
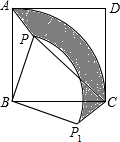如图，已知点P是正方形ABCD内一点，连接PA、PB．将△PAB绕点B沿顺时针方向旋转90°到△P1CB的位置．设AB的长为3，PB的长为2，则△PAB旋转到△P1CB的位置的过程中，边PA所扫过的区域（图中阴影部分）的面积为| 5π |
| 4 |
| 5π |
| 4 |
分析：图中阴影部分的面积等于扇形BAC的面积减去扇形BPP′的面积即可．
解答：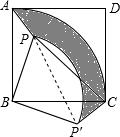
解：连接PP′，
根据旋转的性质可知：△APB≌△CP′B，
则BP=BP′=2，∠PBP′=90°，
阴影部分的面积=S扇形BAC-S扇形BPP′=
-
=
，
故答案为：
．
解：连接PP′，根据旋转的性质可知：△APB≌△CP′B，
则BP=BP′=2，∠PBP′=90°，
阴影部分的面积=S扇形BAC-S扇形BPP′=
| 90π×32 |
| 360 |
| 90π×22 |
| 360 |
| 5π |
| 4 |
故答案为：
| 5π |
| 4 |
点评：本题考查了扇形的面积计算方法，解题的关键是弄清复合图形的面积计算方法．
练习册系列答案
相关题目
，
如图，已知正方形ABCD的边长为4，将正方形置于平面直角坐标系xOy中，使AB在x轴的负半轴上，A点的坐标是（-1，0）．
如图，已知B（0，4），点A在第一象限，且AB⊥y轴，∠A=30°．
如图，已知点A、B、C是数轴上三点，O为原点．点C对应的数为6，BC=4．AB=12．
CQ，设运动时间为t（t＞0）．