题目内容
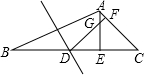（1997•山东）如图，在△ABC中，∠B=22.5°，边AB的垂直平分线交BC于D，DF⊥AC于F，并与BC边上的高AE交于G．求证：EG=EC．分析：连接AD，求出DE=AE，∠GDE=∠CAE，证△DEG≌△AEC，根据全等三角形的性质推出即可．
解答：证明：
连接AD，
∵边AB的垂直平分线交BC于D，
∴BD=AD，
∴∠B=∠BAD=22.5°，
∴∠ADE=22.5°+22.5°=45°，
∵AE⊥BC，
∴∠AEC=∠AED=90°，
∴∠DAE=45°=∠ADE，
∴DE=AE，
∵DF⊥AC，
∴∠DFC=90°=∠AEC，
∴∠ACE+∠FDC=90°，∠ACD+∠CAE=90°，
∴∠CAE=∠FDC，
在△DEG和△AEC中
∴△DEG≌△AEC（ASA），
∴EG=EC．
连接AD，
∵边AB的垂直平分线交BC于D，
∴BD=AD，
∴∠B=∠BAD=22.5°，
∴∠ADE=22.5°+22.5°=45°，
∵AE⊥BC，
∴∠AEC=∠AED=90°，
∴∠DAE=45°=∠ADE，
∴DE=AE，
∵DF⊥AC，
∴∠DFC=90°=∠AEC，
∴∠ACE+∠FDC=90°，∠ACD+∠CAE=90°，
∴∠CAE=∠FDC，
在△DEG和△AEC中
|
∴△DEG≌△AEC（ASA），
∴EG=EC．
点评：本题考查了全等三角形的性质和判定，三角形的外角性质，等腰三角形的性质和判定，三角形的内角和定理等知识点的综合运用．
练习册系列答案
相关题目
（1997•山东）如图，ABCD是一个正方形，P、Q是正方形外两点，且△APD和△BCQ是等边三角形，则∠PQD的正切值是（ ）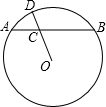
（1997•山东）如图，AB是⊙O的弦，C是弦AB上一点，且BC：CA=2：1，连接OC并延长交⊙O于D，若DC=2cm，OC=3cm，则圆心O到弦AB的距离为（ ）
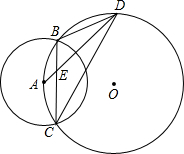（1997•山东）如图，已知A是⊙O上一点，以A为圆心作圆交⊙O于B、C两点，E是弦BC上一点，连接AE并延长⊙O于D，连接BD、CD．设∠BDC=2α．