题目内容
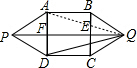
 (1997•山东)如图,ABCD是一个正方形,P、Q是正方形外两点,且△APD和△BCQ是等边三角形,则∠PQD的正切值是( )
(1997•山东)如图,ABCD是一个正方形,P、Q是正方形外两点,且△APD和△BCQ是等边三角形,则∠PQD的正切值是( )分析:连结AQ,通过证明△ABQ≌△DCQ,就可以得出PQ是AD的中垂线,可以得出PQ是BC的中垂线,就可以表示出QE的值,CE的值,就可以求出∠PQD的正切值.
解答:解:连结AQ,
∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠BAD=∠ADC=∠DCB=∠ABC=90°,AD∥BC.
∴∠AFQ=∠BEQ.
∵△APD和△BCQ是等边三角形,
∴PD=PA=AD,BQ=CQ=BC,∠BCQ=∠CBQ=60°,
∴∠DCB+∠BCQ=∠ABC+∠CBQ,
∴∠DCQ=∠ABQ.
∵在△DCQ和△ABQ中,
,
∴△DCQ≌△ABQ(SAS),
∴DQ=AQ.
∵DQ=AP,
∴PQ是AD的中垂线,
∴∠AFQ=∠AFP=90°,DF=
AD,
∴∠BEQ=90°,
∴CE=
BC.
设BC=a,则CE=DF=
a,EF=a,在Rt△QEC中,由勾股定理,得
QE=
a,
∴FQ=a+
a,
∴tan∠PQD=
=2-
.
故选A.
∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠BAD=∠ADC=∠DCB=∠ABC=90°,AD∥BC.
∴∠AFQ=∠BEQ.
∵△APD和△BCQ是等边三角形,
∴PD=PA=AD,BQ=CQ=BC,∠BCQ=∠CBQ=60°,
∴∠DCB+∠BCQ=∠ABC+∠CBQ,
∴∠DCQ=∠ABQ.
∵在△DCQ和△ABQ中,
|
∴△DCQ≌△ABQ(SAS),
∴DQ=AQ.
∵DQ=AP,
∴PQ是AD的中垂线,
∴∠AFQ=∠AFP=90°,DF=
| 1 |
| 2 |
∴∠BEQ=90°,
∴CE=
| 1 |
| 2 |
设BC=a,则CE=DF=
| 1 |
| 2 |
QE=
| ||
| 2 |
∴FQ=a+
| ||
| 2 |
∴tan∠PQD=
| ||||
a+
|
| 3 |
故选A.

点评:本题考查了正方形的性质的运用,全等三角形的判定及性质的运用,勾股定理的运用,锐角三角函数的运用.解答时作出辅助线证明三角形全等是关键.

练习册系列答案
相关题目
 (1997•山东)如图,AB是⊙O的弦,C是弦AB上一点,且BC:CA=2:1,连接OC并延长交⊙O于D,若DC=2cm,OC=3cm,则圆心O到弦AB的距离为( )
(1997•山东)如图,AB是⊙O的弦,C是弦AB上一点,且BC:CA=2:1,连接OC并延长交⊙O于D,若DC=2cm,OC=3cm,则圆心O到弦AB的距离为( ) (1997•山东)如图,在△ABC中,∠B=22.5°,边AB的垂直平分线交BC于D,DF⊥AC于F,并与BC边上的高AE交于G.求证:EG=EC.
(1997•山东)如图,在△ABC中,∠B=22.5°,边AB的垂直平分线交BC于D,DF⊥AC于F,并与BC边上的高AE交于G.求证:EG=EC. (1997•山东)如图,已知A是⊙O上一点,以A为圆心作圆交⊙O于B、C两点,E是弦BC上一点,连接AE并延长⊙O于D,连接BD、CD.设∠BDC=2α.
(1997•山东)如图,已知A是⊙O上一点,以A为圆心作圆交⊙O于B、C两点,E是弦BC上一点,连接AE并延长⊙O于D,连接BD、CD.设∠BDC=2α.