题目内容
某班45学生协商共建“和谐班委”议案,第一轮无记名方式海选出A、B、C、D四名同学;第二轮A、B、C、D中的2名自由组建“和谐班委”轮回值周,用列表或树状图法解决下列问题:
(1)学生A、B获得首次值周的概率是多少?
(2)学生A首次不值周的概率是多少?
(1)学生A、B获得首次值周的概率是多少?
(2)学生A首次不值周的概率是多少?
考点:列表法与树状图法
专题:计算题
分析:(1)列表得出所有等可能的情况数,找出A、B学生获得首次值周的情况数,即可求出所求的概率;
(2)找出A首次不值周的情况数,即可求出所求概率.
(2)找出A首次不值周的情况数,即可求出所求概率.
解答:解:(1)列表如下:
所有等可能的情况有12种,但是这12种中是存在重复的,例如:(A,B)与(B,A)情况是一样的,不存在优先选择,因此所有的情况只有6种;
其中学生A、B获得首次值周的情况有1种,
则P=
;
(2)学生A首次不值周的情况有3种,
则P=
=
.
| A | B | C | D | |
| A | --- | --- | --- | --- |
| B | (A,B) | --- | --- | --- |
| C | (A,C) | (B,C) | --- | --- |
| D | (A,D) | (B,D) | (C,D) | --- |
其中学生A、B获得首次值周的情况有1种,
则P=
| 1 |
| 6 |
(2)学生A首次不值周的情况有3种,
则P=
| 3 |
| 6 |
| 1 |
| 2 |
点评:此题考查了列表法与树状图法,用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
| 1 |
| 2 |
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
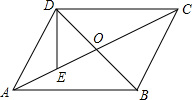 在平行四边形ABCD中,对角线AC、BD交于点O,AD=AO,点E为OA中点.
在平行四边形ABCD中,对角线AC、BD交于点O,AD=AO,点E为OA中点.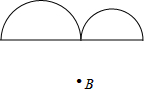 画出如图所示的两个半圆关于点B成中心对称的图形.
画出如图所示的两个半圆关于点B成中心对称的图形.