题目内容
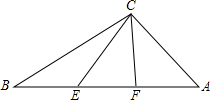 如图,从直角△ABC的直角顶点C作斜边AB的三等分点的连线CE、CF.已知CE=sinθ,CF=cosθ(θ为锐角),则AB=
如图,从直角△ABC的直角顶点C作斜边AB的三等分点的连线CE、CF.已知CE=sinθ,CF=cosθ(θ为锐角),则AB=分析:作EM⊥BC,FN⊥BC,设AB=3x则BE=EF=FA=x;设BC=3y则BM=MN=NC=y,2ME=NF,利用勾股定理分别列出:ME2+MC2=EC2,NF2+NC2=FC2,然后将两式相加,求得BE的长即可求得AB的长.
解答: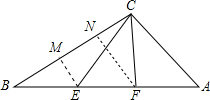 解:作EM⊥BC,FN⊥BC.
解:作EM⊥BC,FN⊥BC.
∵∠C=90°,
∴∠BME=∠BNF=90°,
设AB=3x则BE=EF=FA=x
设BC=3y则BM=MN=NC=y,2ME=NF,
在Rt△CME中,ME2+MC2=EC2,即ME2+4y2=sin2α.(1)
在Rt△CNF中,NF2+NC2=FC2,即4ME2+y2=cos2α.(2)
(1)+(2)得:5ME2+5y2=1,ME2+y2=
,
在Rt△BME中:BE2=BM2+ME2,即:x2=y2+ME2=
,
∴AB=3BE=
.
故答案为:
.
 解:作EM⊥BC,FN⊥BC.
解:作EM⊥BC,FN⊥BC.∵∠C=90°,
∴∠BME=∠BNF=90°,
设AB=3x则BE=EF=FA=x
设BC=3y则BM=MN=NC=y,2ME=NF,
在Rt△CME中,ME2+MC2=EC2,即ME2+4y2=sin2α.(1)
在Rt△CNF中,NF2+NC2=FC2,即4ME2+y2=cos2α.(2)
(1)+(2)得:5ME2+5y2=1,ME2+y2=
| 1 |
| 5 |
在Rt△BME中:BE2=BM2+ME2,即:x2=y2+ME2=
| 1 |
| 5 |
∴AB=3BE=
3
| ||
| 5 |
故答案为:
3
| ||
| 5 |
点评:此题主要考查学生对勾股定理和锐角三角函数等知识点的理解和掌握,解答此题的关键是设AB=3x则BE=EF=FA=x;设BC=3y则BM=MN=NC=y,2ME=NF,此题难度较大,属于难题.

练习册系列答案
相关题目
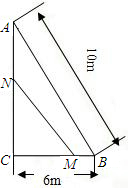 如图,在直角△ABC中,∠C=90°,BC=6m,AB=10m.点M从B点以1m/s的速度向点C匀速移动,同时点N从C点以2m/s的速度向点A匀速移动,问几秒钟后,△MNC的面积是△ABC面积的
如图,在直角△ABC中,∠C=90°,BC=6m,AB=10m.点M从B点以1m/s的速度向点C匀速移动,同时点N从C点以2m/s的速度向点A匀速移动,问几秒钟后,△MNC的面积是△ABC面积的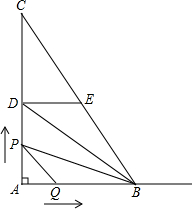 秒2个单位长的速度匀速运动,当点P与点B重合时停止运动,点Q也随之停止运动,设点P、Q运动时间是t秒,(t>0)
秒2个单位长的速度匀速运动,当点P与点B重合时停止运动,点Q也随之停止运动,设点P、Q运动时间是t秒,(t>0)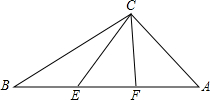 如图,从直角△ABC的直角顶点C作斜边AB的三等分点的连线CE、CF.已知CE=sinθ,CF=cosθ(θ为锐角),则AB=________.
如图,从直角△ABC的直角顶点C作斜边AB的三等分点的连线CE、CF.已知CE=sinθ,CF=cosθ(θ为锐角),则AB=________.