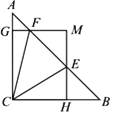
题目内容
【题目】在一次数学兴趣小组活动中,小明利用“同弧所对的圆周角及圆心角的性质”探索了一些问题,下面请你和小明一起进入探索之旅.
问题情境:
(1)如图1,在△ABC中,∠A=30°,BC=2,则△ABC的外接圆的半径为 .
操作实践:
(2)如图2,在矩形ABCD中,请利用以上操作所获得的经验,在矩形ABCD内部用直尺与圆规作出一点P.点P满足:∠BPC=∠BEC,且PB=PC.(要求:用直尺与圆规作出点P,保留作图痕迹.)
迁移应用:
(3)如图3,在平面直角坐标系的第一象限内有一点B,坐标为(2,m).过点B作AB⊥y轴,BC⊥x轴,垂足分别为A、C,若点P在线段AB上滑动(点P可以与点A、B重合),发现使得∠OPC=45°的位置有两个,则m的取值范围为 .
【答案】(1)2;(2)作图见解析;(3)2≤m<1+![]()
【解析】试题分析:(1)连接OB、OC,只要证明△OBC是等边三角形即可.
(2)如图2中,作BC的垂直平分线,交BE于点O,以O为圆心,OB为半径作圆,交垂直平分线于点P,则点P为所求.
(3)如图3中,在x轴上方作△OKC,使得△OKC是以OC为斜边的等腰直角三角形,作KE⊥AB于E.当EK=KC=![]() 时,以K为圆心,KC为半径的圆与AB相切,此时m=BC=1+
时,以K为圆心,KC为半径的圆与AB相切,此时m=BC=1+![]() ,在AB上只有一个点P满足∠OPC=
,在AB上只有一个点P满足∠OPC=![]() ∠OKC=45°,当BK=
∠OKC=45°,当BK=![]() 时,在AB上恰好有两个点P满足∠OPC=
时,在AB上恰好有两个点P满足∠OPC=![]() ∠OKC=45°,此时m=BC=2,由此不难得出结论.
∠OKC=45°,此时m=BC=2,由此不难得出结论.
解:(1)如图1中,连接OB、OC.

∵∠BOC=2∠A,∠A=30°,
∴∠BOC=60°,
∵OB=OC,
∴△OBC是等边三角形,
∴OB=OC=BC=2,
故答案为:2;
(2)如图2中,作BC的垂直平分线,交BE于点O;
以O为圆心,OB为半径作圆,交垂直平分线于点P,
则点P为所求.

(3)如图3中,在x轴上方作△OKC,使得△OKC是以OC为斜边的等腰直角三角形,作KE⊥AB于E.
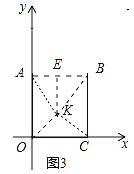
∵OC=2,
∴OK=KC=![]() ,
,
当EK=KC=![]() 时,以K为圆心,KC为半径的圆与AB相切,此时m=BC=1+
时,以K为圆心,KC为半径的圆与AB相切,此时m=BC=1+![]() ,在AB上只有一个点P满足∠OPC=
,在AB上只有一个点P满足∠OPC=![]() ∠OKC=45°,
∠OKC=45°,
当BK=![]() 时,在AB上恰好有两个点P满足∠OPC=
时,在AB上恰好有两个点P满足∠OPC=![]() ∠OKC=45°,此时m=BC=2,
∠OKC=45°,此时m=BC=2,
综上所述,满足条件的m的值的范围为2≤m<1+![]() .
.
故答案为2≤m<1+![]() .
.

 53随堂测系列答案
53随堂测系列答案【题目】某超市电器销售每台进价分别为200元、170元的A、B两种型号的电风扇,下表是近两周的销售情况:
销售时段 | 销售量 | 销售收入 | |
A型号 | B型号 | ||
第一周 | 3台 | 5台 | 1800元 |
第二周 | 4台 | 10台 | 3100元 |
(1)求A、B两种型号的电风扇的销售价.
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇30台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能请给出采购方案.若不能,请说明理由.
【题目】为了将十堰打造成区域中心城市,实现跨越式发展,我市郧阳区建设正按投资计划有序推进.因道路建设需要开挖土石方,计划每小时挖掘土石方270m3,现决定向某大型机械租赁公司租用甲、乙两种型号的挖掘机来完成这项工作,租赁公司提供的挖掘机有关信息如表:
租金(单位:元/台时) | 挖掘土石方量(单位:m3/台时) | |
甲型挖掘机 | 200 | 30 |
乙型挖掘机 | 260 | 40 |
(1)若租用甲、乙两种型号的挖掘机共8台,恰好完成每小时的挖掘量,则甲、乙两种型号的挖掘机各需多少台?
(2)如果每小时支付的租金不超过1780元,又恰好完成每小时的挖掘量,那么共有几种不同的租用方案?