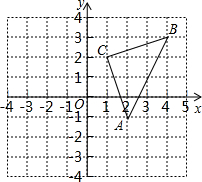题目内容
在平面直角坐系中,已知O为原点,在长方形ABCD中,A、B、C坐标分别是A(-3,1),B(-3,3),C(2,3)
(1)求D坐标;
(2)将长方形以每秒1个单位长度的速度水平向右平移2秒后得四边形A1B1C1D1的顶点坐标是多少?请将(1),(2)答案填下表;
(3)平移(2)中长方形ABCD,几秒钟后△OBD面积为长方形ABCD的面积的
?
(1)求D坐标;
(2)将长方形以每秒1个单位长度的速度水平向右平移2秒后得四边形A1B1C1D1的顶点坐标是多少?请将(1),(2)答案填下表;
(3)平移(2)中长方形ABCD,几秒钟后△OBD面积为长方形ABCD的面积的
| 3 |
| 2 |
| 点 | D | A1 | B1 | C1 | D1 |
| 坐标 |
(1)∵B、C两点纵坐标相等,∴BC∥x轴
又∵BC∥AD,∴A、D两点纵坐标相等,都是1,
同理,得C、D两点横坐标相等,都是2;
故D(2,1).
(2)
(3)
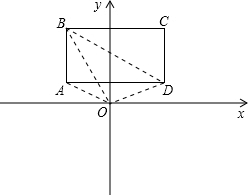
设x秒后△OBD面积为ABCD的
A(-3+x,1),B(-3+x,3),C(2+x,3),D(2+x,1)
连OA,则S△OBD=S△OAD-S△OBA+S△ABD
=
×5×1-
×2|x-3|+
×2×5=
-|x-3|+5
=
-|x-3|
即
-|x-3|=2×5×
∴x=10.5或x=-
(舍去)
答:10.5秒钟后△OBD面积为长方形ABCD的面积的
.
又∵BC∥AD,∴A、D两点纵坐标相等,都是1,
同理,得C、D两点横坐标相等,都是2;
故D(2,1).
(2)
| 点 | D | A1 | B1 | C1 | D1 |
| 坐标 | (2,1) | (-1,1) | (-1,3) | (4,3) | (4,1) |

设x秒后△OBD面积为ABCD的
| 3 |
| 2 |
A(-3+x,1),B(-3+x,3),C(2+x,3),D(2+x,1)
连OA,则S△OBD=S△OAD-S△OBA+S△ABD
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
=
| 15 |
| 2 |
即
| 15 |
| 2 |
| 3 |
| 2 |
∴x=10.5或x=-
| 9 |
| 2 |
答:10.5秒钟后△OBD面积为长方形ABCD的面积的
| 3 |
| 2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目