题目内容
（2007•台湾）如图，平行四边形ABCD中，BC=12，M为BC中点，M到AD的距离为8．若分别以B、C为圆心，BM长为半径画弧，交AB、CD于E、F两点，则图中斜线区域面积为（ ）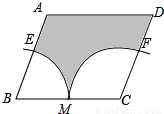
A．96-12π
B．96-18π
C．96-24π
D．96-27π
【答案】分析：由平行四边形的邻角互补，可知：∠B与∠C的度数和为180°，而扇形BEM和扇形CMF的半径相等，因此两个扇形的面积和正好是一个半圆的面积，因此阴影部分的面积可用?ABCD和以BM为半径的半圆的面积差来求得．
解答：解：∵四边形ABCD是平行四边形
∴∠B+∠C=180°，
∴S扇形BEM+S扇形CMF=
π•62=18π，
∴S阴影=S?ABCD-（S扇形BEM+S扇形CMF）=12×8-18π=96-18π．
故选B．
点评：此题主要考查平行四边形的性质和扇形面积的计算．
解答：解：∵四边形ABCD是平行四边形
∴∠B+∠C=180°，
∴S扇形BEM+S扇形CMF=
π•62=18π，∴S阴影=S?ABCD-（S扇形BEM+S扇形CMF）=12×8-18π=96-18π．
故选B．
点评：此题主要考查平行四边形的性质和扇形面积的计算．
练习册系列答案
相关题目
