题目内容
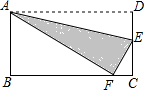
如图，在矩形ABCD中，AB=4，AD=5，将点D折叠至边BC上的F处，折痕为AF，试求图中阴影部分的面积．
∵四边形ABCD是矩形，
∴CD=AB=4，BC=AD=5，∠B=∠C=90°，
由折叠的性质可得：AF=AD=5，DE=EF，
∴在Rt△ABF中，BC=
=3，
∴CF=2，
设DE=x，则EF=x，EC=4-x，
在Rt△ECF中，EF2=EC2+FC2，
即x2=22+（4-x）2，
解得：x=
，
∴DE=
．
∴S阴影=S矩形ABCD-2S△ADE=4×5-2×
×5×
=
．
∴CD=AB=4，BC=AD=5，∠B=∠C=90°，
由折叠的性质可得：AF=AD=5，DE=EF，
∴在Rt△ABF中，BC=
| AF2-AB2 |
∴CF=2，
设DE=x，则EF=x，EC=4-x，
在Rt△ECF中，EF2=EC2+FC2，
即x2=22+（4-x）2，
解得：x=
| 5 |
| 2 |
∴DE=
| 5 |
| 2 |
∴S阴影=S矩形ABCD-2S△ADE=4×5-2×
| 1 |
| 2 |
| 5 |
| 2 |
| 15 |
| 2 |
练习册系列答案
阅读快车系列答案
相关题目
