题目内容
【题目】如图,二次函数 ![]() 的图象经过点A(4,0),B(﹣4,﹣4),且与y轴交于点C.
的图象经过点A(4,0),B(﹣4,﹣4),且与y轴交于点C.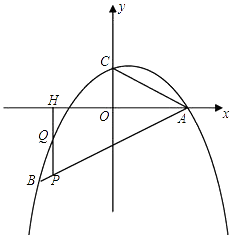
(1)试求此二次函数的解析式;
(2)试证明:∠BAO=∠CAO(其中O是原点);
(3)若P是线段AB上的一个动点(不与A、B重合),过P作y轴的平行线,分别交此二次函数图象及x轴于Q、H两点,试问:是否存在这样的点P,使PH=2QH?若存在,请求出点P的坐标;若不存在,请说明理由.
【答案】
(1)解:∵点A(4,0)与B(﹣4,﹣4)在二次函数图象上,
∴ ![]()
解得 ![]()
∴二次函数解析式为y=﹣ ![]() x2+
x2+ ![]() x+2.
x+2.
(2)解:过B作BD⊥x轴于点D,由(1)得C(0,2),
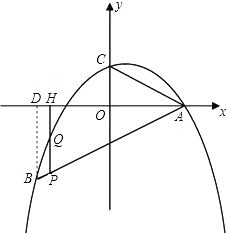
则在Rt△AOC中,tan∠CAO= ![]() =
= ![]() =
= ![]() ,
,
又在Rt△ABD中,tan∠BAD= ![]() =
= ![]() =
= ![]() ;
;
∵tan∠CAO=tan∠BAD,
∴∠CAO=∠BAO.
(3)解:由点A(4,0)与B(﹣4,﹣4),可得直线AB的解析式为y= ![]() x﹣2,
x﹣2,
设P(x, ![]() x﹣2),(﹣4<x<4);
x﹣2),(﹣4<x<4);
则Q(x,﹣ ![]() x2+
x2+ ![]() x+2),
x+2),
∴PH=| ![]() x﹣2|=2﹣
x﹣2|=2﹣ ![]() x,QH=|﹣
x,QH=|﹣ ![]() x2+
x2+ ![]() x+2|.
x+2|.
∴2﹣ ![]() x=2|﹣
x=2|﹣ ![]() x2+
x2+ ![]() x+2|.
x+2|.
当2﹣ ![]() x=﹣
x=﹣ ![]() x2+x+4,
x2+x+4,
解得x1=﹣1,x2=4(舍去),
∴P(﹣1,﹣ ![]() )
)
当2﹣ ![]() x=
x= ![]() x2﹣x﹣4,
x2﹣x﹣4,
解得x1=﹣3,x2=4(舍去),
∴P(﹣3,﹣ ![]() ).
).
综上所述,存在满足条件的点,它们是P1(﹣1,﹣ ![]() )与P2(﹣3,﹣
)与P2(﹣3,﹣ ![]() ).
).
【解析】(1)利用待定系数法把AB坐标代入抛物线解析式即可;(2)求出这两个锐角的正切值,反过来由值相等可以推得角相等;(3)竖直线段的长可转化为y上-y下,HQ的长可分类讨论HQ=yH-yQ或HQ=yQ-yH,即可求出结果.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目