题目内容
如图1,直线AB上有一点P,点M、N分别为线段PA、PB的中点,AB=14.
(1)若点P在线段AB上,且AP=8,求线段MN的长度;
(2)若点P在直线AB上运动,试说明线段MN的长度与点P在直线AB上的位置无关;
(3)如图2,若点C为线段AB的中点,点P在线段AB的延长线上,下列结论:①
的值不变;②
的值不变,请选择一个正确的结论并求其值.

(1)若点P在线段AB上,且AP=8,求线段MN的长度;
(2)若点P在直线AB上运动,试说明线段MN的长度与点P在直线AB上的位置无关;
(3)如图2,若点C为线段AB的中点,点P在线段AB的延长线上,下列结论:①
| PA-PB |
| PC |
| PA+PB |
| PC |
分析:(1)求出MP,NP的长度,即可得出MN的长度;
(2)分三种情况:①点P在AB之间;②点P在AB的延长线上;③点P在BA的延长线上,分别表示出MN的长度即可作出判断;
(3)设AC=BC=x,PB=y,分别表示出①、②的值,继而可作出判断.
(2)分三种情况:①点P在AB之间;②点P在AB的延长线上;③点P在BA的延长线上,分别表示出MN的长度即可作出判断;
(3)设AC=BC=x,PB=y,分别表示出①、②的值,继而可作出判断.
解答:解:(1)∵AP=8,点M是AP中点,
∴MP=
AP=4,
∴BP=AB-AP=6,
又∵点N是PB中点,
∴PN=
PB=3,
∴MN=MP+PN=7.
(2)①点P在AB之间;②点P在AB的延长线上;③点P在BA的延长线上,均有MN=
AB=7.
(3)选择②.
设AC=BC=x,PB=y,
①
=
=
(在变化);
②
=
=2(定值).
∴MP=
| 1 |
| 2 |
∴BP=AB-AP=6,
又∵点N是PB中点,
∴PN=
| 1 |
| 2 |
∴MN=MP+PN=7.
(2)①点P在AB之间;②点P在AB的延长线上;③点P在BA的延长线上,均有MN=
| 1 |
| 2 |
(3)选择②.
设AC=BC=x,PB=y,
①
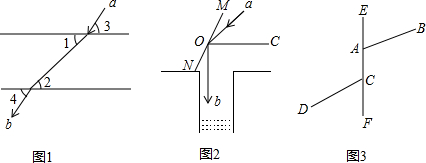
| PA-PB |
| PC |
| AB |
| x+y |
| 14 |
| x+y |
②
| PA+PB |
| PC |
| 2x+2y |
| x+y |
点评:本题考查了两点间的距离,解答本题注意分类讨论思想的运用,理解线段中点的定义,难度一般.

练习册系列答案
相关题目


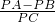 的值不变;②
的值不变;②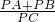 的值不变,请选择一个正确的结论并求其值.
的值不变,请选择一个正确的结论并求其值.