题目内容
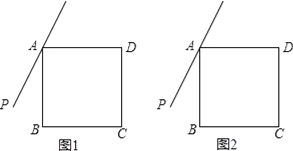
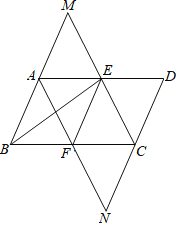
【题目】如图,在ABCD中,AF是∠BAD的平分线,交BC于点F,与DC的延长线交于点N.CE是∠BCD的平分线,交AD于点E,与BA的延长线交于点M.
(1)试判断四边形AFCE的形状,并说明理由;
(2)若BE⊥ME,证明四边形ABFE是菱形.
【答案】(1)四边形AFCE是平行四边形,理由见解析;(2)见解析.
【解析】
(1)四边形AFCE的形状是平行四边形,利用已知条件证明AF∥CE即可;
(2)先证明BA=AE,BF=AE,再证明四边形ABFE的是平行四边形,即可解答
(1)四边形AFCE是平行四边形,
理由如下:∵四边形ABCD是平行四边形,
∴∠BAD=∠BCD,AD∥BC,
∴∠FAD=∠BFA.
∵AF是∠BAD的角平分线,CE是∠BCD的角平分线,
∴∠FAD=![]() ∠BAD,∠BCE=
∠BAD,∠BCE=![]() ∠BCD,
∠BCD,
∴∠FAD=∠BCE,
∴∠BFA=∠BCE,
∴AF∥CE,
又∵AD∥BC,
∴四边形AFCE的是平行四边形;
(2)∵AF是∠BAD的角平分线,且∠FAD=∠BFA,
∴∠BFA=∠BAF,
∴BA=BF,
∵BE⊥ME,
∴∠BEM=90°,
∵AF∥CE,
∴∠BOA=∠BEM=90°,即BO⊥AF,
又∵在△ABF中,BA=BF,
∴∠ABE=∠FBE,
∵AD∥BC,
∴∠AEB=∠FBE,
∴∠ABE=∠AEB,
∴BA=AE,
∴BF=AE,
又∵AD∥BC,
∴四边形ABFE的是平行四边形,
又∵BA=BF,
∴ABFE是菱形.

 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
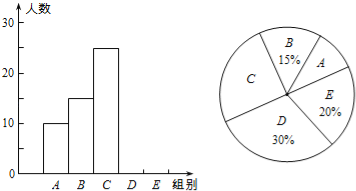
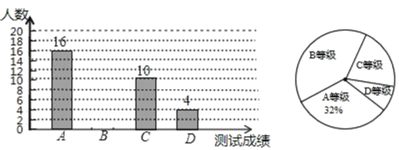
超能学典应用题题卡系列答案【题目】某校举行“汉字听写”比赛,每位学生听写汉字39个,比赛结束后随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分.
组别 | 正确字数x | 人数 |
A | 0≤x<8 | 10 |
B | 8≤x<16 | 15 |
C | 16≤x<24 | 25 |
D | 24≤x<32 | m |
E | 32≤x<40 | n |
根据以上信息解决下列问题:
(1)在统计表中,m= ,n= ,并补全条形统计图.
(2)扇形统计图中“C组”所对应的圆心角的度数是 .
(3)若该校共有900名学生,如果听写正确的个数少于24个定为不合格,请你估计这所学校本次比赛听写不合格的学生人数.