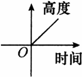
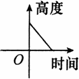
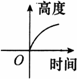
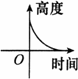
题目内容
| |||||
答案:
解析:
解析:
|
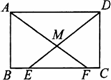
证明:∵BE=CF, ∴BE+EF=CF+EF,即BF=CE. ∵四边形ABCD为矩形, ∴∠B=∠C=90°,AB=DC, ∴△ABF≌△DCE, ∴∠MFE=∠MEF,且AF=DE, 由∠MFE=∠MEF,知MF=ME, ∴AF-MF=DE-ME,即AM=DM. |

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目