题目内容
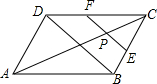 (2013•门头沟区二模)如图,在平行四边形ABCD中,AC=12,BD=8,P是AC上的一个动点,过点P作EF∥BD,与平行四边形的两条边分别交于点E、F.设CP=x,EF=y,则下列图象中,能表示y与x的函数关系的图象大致是( )
(2013•门头沟区二模)如图,在平行四边形ABCD中,AC=12,BD=8,P是AC上的一个动点,过点P作EF∥BD,与平行四边形的两条边分别交于点E、F.设CP=x,EF=y,则下列图象中,能表示y与x的函数关系的图象大致是( )分析:AC与BD相交于O,分类讨论:当点P在OC上时,根据平行四边形的性质得OC=OA=
AC=6,利用EF∥BD得△CEF∽△CBD,根据相似比可得到y=
x(0≤x≤6);
当点P在OA上时,AP=12-x,由EF∥BD得△AEF∽△ABD,据相似比可得到y=-
x+16(6<x≤12),然后根据函数解析式对各选项分别进行判断.
| 1 |
| 2 |
| 4 |
| 3 |
当点P在OA上时,AP=12-x,由EF∥BD得△AEF∽△ABD,据相似比可得到y=-
| 4 |
| 3 |
解答:解:AC与BD相交于O,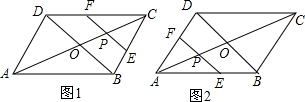
当点P在OC上时,如图1
∵四边形ABCD为平行四边形,
∴OC=OA=
AC=6,
∵EF∥BD,
∴△CEF∽△CBD,
∴
=
,即
=
,
∴y=
x(0≤x≤6);
当点P在OA上时,如图2,
则AP=12-x,
∵EF∥BD,
∴△AEF∽△ABD,
∴
=
,即
=
,
∴y=-
x+16(6<x≤12),
∴y与x的函数关系的图象由正比例函数y=
x(0≤x≤6)的图象和一次函数y=-
x+16(6<x≤12)组成.
故选D.

当点P在OC上时,如图1
∵四边形ABCD为平行四边形,
∴OC=OA=
| 1 |
| 2 |
∵EF∥BD,
∴△CEF∽△CBD,
∴
| EF |
| BD |
| CP |
| OC |
| y |
| 8 |
| x |
| 6 |
∴y=
| 4 |
| 3 |
当点P在OA上时,如图2,
则AP=12-x,
∵EF∥BD,
∴△AEF∽△ABD,
∴
| EF |
| BD |
| AP |
| AO |
| y |
| 8 |
| 12-x |
| 6 |
∴y=-
| 4 |
| 3 |
∴y与x的函数关系的图象由正比例函数y=
| 4 |
| 3 |
| 4 |
| 3 |
故选D.
点评:本题考查了动点问题的函数图象:利用点运动的几何性质列出有关的函数关系式,然后根据函数关系式画出函数图象,注意自变量的取值范围.

练习册系列答案
相关题目
 (2013•门头沟区二模)某中学初三年级的学生开展测量物体高度的实践活动,他们要测量一幢建筑物AB的高度.如图,他们先在点C处测得建筑物AB的顶点A的仰角为30°,然后向建筑物AB前进20m到达点D处,又测得点 A的仰角为60°,则建筑物AB的高度是
(2013•门头沟区二模)某中学初三年级的学生开展测量物体高度的实践活动,他们要测量一幢建筑物AB的高度.如图,他们先在点C处测得建筑物AB的顶点A的仰角为30°,然后向建筑物AB前进20m到达点D处,又测得点 A的仰角为60°,则建筑物AB的高度是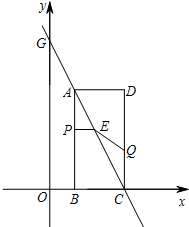 (2013•门头沟区二模)如图,在平面直角坐标系xOy中,已知矩形ABCD的两个顶点B、C的坐标分别是B(1,0)、C(3,0).直线AC与y轴交于点G(0,6).动点P从点A出发,沿线段AB向点B运动.同时动点 Q从点C出发,沿线段CD向点D运动.点P、Q的运动速度均为每秒1个单位,运动时间为t秒.过点P作PE⊥AB交AC于点E.
(2013•门头沟区二模)如图,在平面直角坐标系xOy中,已知矩形ABCD的两个顶点B、C的坐标分别是B(1,0)、C(3,0).直线AC与y轴交于点G(0,6).动点P从点A出发,沿线段AB向点B运动.同时动点 Q从点C出发,沿线段CD向点D运动.点P、Q的运动速度均为每秒1个单位,运动时间为t秒.过点P作PE⊥AB交AC于点E.