题目内容
【题目】已知![]() 为等边三角形,
为等边三角形,![]() 为射线
为射线![]() 上一点,
上一点,![]() 为射线
为射线![]() 上一点,
上一点,![]() .
.
(1)如图1,当点![]() 在
在![]() 的延长线上且
的延长线上且![]() 时,
时,![]() 是
是![]() 的中线吗?请说明理由;
的中线吗?请说明理由;
(2)如图2,当点![]() 在
在![]() 的延长线上时,写出
的延长线上时,写出![]() 之间的数量关系,请说明理由;
之间的数量关系,请说明理由;
(3)如图3,当点![]() 在线段
在线段![]() 的延长线上,点
的延长线上,点![]() 在线段
在线段![]() 上时,请直接写出
上时,请直接写出![]() 的数量关系.
的数量关系.

【答案】(1)![]() 是
是![]() 的中线,理由详见解析;(2)
的中线,理由详见解析;(2)![]() ,理由详见解析;(3)
,理由详见解析;(3)![]() .
.
【解析】
(1)利用△ABC是等边三角形及CD=CE可得∠CDE=∠E=30°,利用AD=DE,证明∠CAD=∠E =30°,即可解决问题.
(2)在AB上取BH=BD,连接DH,证明AHD≌△DCE得出DH=CE,得出AE=AB+BD,
(3)在AB上取AF=AE,连接DF,利用△AFD≌△EFD得出角的关系,得出△BDF是等腰三角形,根据边的关系得出结论AB=BD+AE.
(1)解:如图1,结论:AD是△ABC的中线.理由如下: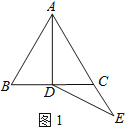
∵△ABC是等边三角形,
∴AB=AC,∠BAC=∠B=∠ACB=60°,
∵CD=CE,
∴∠CDE=∠E,
∵∠ACD=∠CDE+∠E=60°,
∴∠E=30°,
∵DA=DE,
∴∠DAC=∠E=30°,
∵∠BAC=60°,
∴∠DAB=∠CAD,
∵AB=AC,
∴BD=DC,
∴AD是△ABC的中线.
(2)结论:AB+BD=AE,理由如下:
如图2,在AB上取BH=BD,连接DH,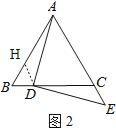
∵BH=BD,∠B=60°,
∴△BDH为等边三角形,AB-BH=BC-BD,
∴∠BHD=60°,BD=DH,AH=DC,
∵AD=DE,
∴∠E=∠CAD,
∴∠BAC-∠CAD=∠ACB-∠E
∴∠BAD=∠CDE,
∵∠BHD=60°,∠ACB=60°,
∴180°-∠BHD=180°-∠ACB,
∴∠AHD=∠DCE,
∴在△AHD和△DCE,
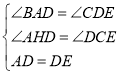
∴△AHD≌△DCE(AAS),
∴DH=CE,
∴BD=CE,
∴AE=AC+CE=AB+BD.
(3)结论:AB=BD+AE,理由如下:
如图3,在AB上取AF=AE,连接DF,
∵△ABC为等边三角形,
∴∠BAC=∠ABC=60°,
∴△AFE是等边三角形,
∴∠FAE=∠FEA=∠AFE=60°,
∴EF∥BC,
∴∠EDB=∠DEF,
∵AD=DE,
∴∠DEA=∠DAE,
∴∠DEF=∠DAF,
∵DF=DF,AF=EF,
在△AFD和△EFD中,
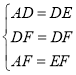 ,
,
∴△AFD≌△EFD(SSS)
∴∠ADF=∠EDF,∠DAF=∠DEF,
∴∠FDB=∠EDF+∠EDB,∠DFB=∠DAF+∠ADF,
∵∠EDB=∠DEF,
∴∠FDB=∠DFB,
∴DB=BF,
∵AB=AF+FB,
∴AB=BD+AE.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案【题目】在“朗读者”节目的影响下,某中学开展了“好书伴我成长”的读书活动,为了解3月份七年级300名学生读书情况,随机调查了七年级50个学生读书的册数,统计数据如下表所示:
册数 | 0 | 1 | 2 | 3 | 4 |
人数 | 4 | 12 | 16 | 17 | 1 |
关于这组数据,下列说法正确的是( )
A. 众数是 17 B. 平均数是 2 C. 中位数是 2 D. 方差是 2







