题目内容
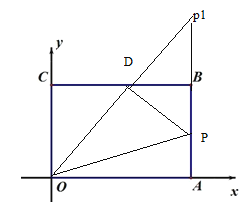
【题目】已知:如图,平面直角坐标系中,矩形OABC的顶点A(6,0)、B(6,4),D是BC的中点.动点P从O点出发,以每秒1个单位的速度,沿着OA、AB、BD运动.设P点运动的时间为t秒(0<t<13).

(1)写出△POD的面积S与t之间的函数关系式,并求出△POD的面积等于9时点P的坐标;
(2)当点P在OA上运动时,连结CP.问:是否存在某一时刻t,当CP绕点P旋转时,点C能恰好落到AB的中点M处?若存在,请求出t的值并判断此时△CPM的形状;若不存在,请说明理由;
(3)当点P在AB上运动时,试探索当PO+PD的长最短时的直线PD的表达式。
【答案】(1)(4.5,0)(2,4)(2)存在(3)y=-![]()
【解析】
试题分析:(1)根据矩形的性质得OA=BC=6,CD=BD=3,AB=4,然后分三种情况求解:当0<t≤6,如图1,OP=t,根据三角形面积公式得S=2t,再求出S=9所对应的t的值,然后写出此时P点坐标;当6<t≤10,如图2,则AP=t-6,BP=10-t,利用S=S矩形ABCD-S△OCD-S△OAP-S△BPD得到S=-![]() t+21,再求出S=9所对应的t的值,然后写出此时P点坐标;当10<t<13,如图3,则PB=13-t,根据三角形的面积公式得S=-2t+26,由于S=9时,计算出t=7.5,而7.5不合题意故舍去;
t+21,再求出S=9所对应的t的值,然后写出此时P点坐标;当10<t<13,如图3,则PB=13-t,根据三角形的面积公式得S=-2t+26,由于S=9时,计算出t=7.5,而7.5不合题意故舍去;
(2)如图4,E点为AB的中点,根据旋转的性质得PC=PE,在Rt△POC中,利用勾股定理得PC2=t2+42;在Rt△PAE中,利用勾股定理得到PE2=(6-t)2+22,则t2+42=(6-t)2+22,解方程得t=2.
(3)根据对称性找到P点的对称点P1,找到D点,然后求出D点的坐标,再根据待定系数法求出解析式.
试题解析:(1)∵矩形OABC的顶点A(6,0)、B(6,4),D是BC的中点,
∴OA=BC=6,CD=BD=3,AB=4,
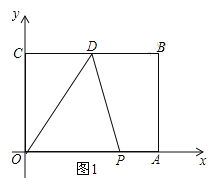
当点P在OA上运动时,即0<t≤6,如图1,OP=t,S=![]() t4=2t;
t4=2t;
∵S=9,
∴2t=9,解得t=4.5,
∴此时P点坐标为(4.5,0);
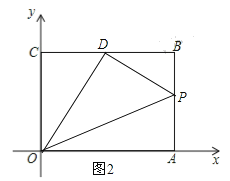
当点P在AB上运动时,即6<t≤10,如图2,AP=t-6,BP=10-t,S=S矩形ABCD-S△OCD-S△OAP-S△BPD
=4×6-![]() 4×3-
4×3-![]() 6(t-6)-
6(t-6)-![]() 3(10-t)
3(10-t)
=-![]() t+21;
t+21;
∵S=9,
∴-![]() t+21=9,解得t=8,
t+21=9,解得t=8,
∴此时P点坐标为(2,4);
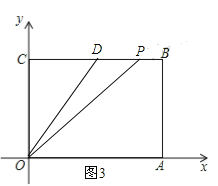
当点P在BD上运动时,即10<t<13,如图3,PB=13-t,S=![]() (13-t)4=-2t+26;
(13-t)4=-2t+26;
∵S=9,
∴-2t+26=9,解得t=7.5(不合题意舍去);
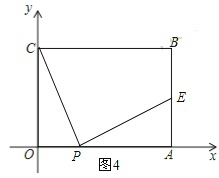
(2)存在.
如图4,E点为AB的中点,
∵CP绕点P旋转时,点C能恰好落到AB的中点,
∴PC=PE,
在Rt△POC中,OC=4,OP=t,
∴PC2=OP2+OC2=t2+42,
在Rt△PAE中,AE=2,PA=6-t,
∴PE2=PA2+AE2=(6-t)2+22,
∴t2+42=(6-t)2+22,解得t=2,
即当t=2s时,当CP绕点P旋转时,点C能恰好落到AB的中点处.
(3)y=-