题目内容
△ABC与△A′B′C′满足下列条件,△ABC与△A′B′C′不一定相似的是
- A.∠A=∠A′=45°38′,∠C=26°22′,∠C′=108°
- B.AB=1,AC=1.5,BC=2,A′B′=12,B′C′=8,A′C′=16
- C.BC=a,AC=b,AB=c,A′B′=
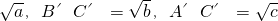
- D.AB=AC,A′B′=A′C′,∠A=∠A′=40°
C
分析:根据相似三角形的判定方法对各个选项进行分析,从而得到最后答案.
解答:A项满足三个角对应相等的条件;
B项满足三边对应成比例;
D项满足两边对应成比例且夹角相等;
只有C不满足任何一个条件;
故选C.
点评:考查相似三角形的判定定理:
(1)两角对应相等的两个三角形相似.
(2)两边对应成比例且夹角相等的两个三角形相似.
(3)三边对应成比例的两个三角形相似.
(4)如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似.
分析:根据相似三角形的判定方法对各个选项进行分析,从而得到最后答案.
解答:A项满足三个角对应相等的条件;
B项满足三边对应成比例;
D项满足两边对应成比例且夹角相等;
只有C不满足任何一个条件;
故选C.
点评:考查相似三角形的判定定理:
(1)两角对应相等的两个三角形相似.
(2)两边对应成比例且夹角相等的两个三角形相似.
(3)三边对应成比例的两个三角形相似.
(4)如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
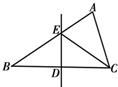 19、如图,在△ABC中,BC边上的垂直平分线DE交边BC于点D,交边AB于点E.若△EDC的周长为24,△ABC与四边形AEDC的周长之差为12,则线段DE的长为
19、如图,在△ABC中,BC边上的垂直平分线DE交边BC于点D,交边AB于点E.若△EDC的周长为24,△ABC与四边形AEDC的周长之差为12,则线段DE的长为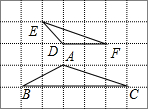 在方格纸中,每个小格的顶点叫做格点,以格点连线为边的图形叫做格点图形.如图,方格网的小方格的边长为1的正方形,试判断格点图形△ABC与△DEF是否相似,并说明你的理由.
在方格纸中,每个小格的顶点叫做格点,以格点连线为边的图形叫做格点图形.如图,方格网的小方格的边长为1的正方形,试判断格点图形△ABC与△DEF是否相似,并说明你的理由.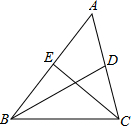 如图,△ABC中,BD、CE是中线,BC=8cm,△ABC与△AEC的周长之差为6cm,△ABD与△BDC的周长之差为2cm,则△BEC的周长为( )
如图,△ABC中,BD、CE是中线,BC=8cm,△ABC与△AEC的周长之差为6cm,△ABD与△BDC的周长之差为2cm,则△BEC的周长为( ) 如图,△ABC与△CDE均是等边三角形,若∠AEB=145°,则∠DBE的度数是
如图,△ABC与△CDE均是等边三角形,若∠AEB=145°,则∠DBE的度数是