题目内容
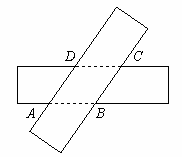
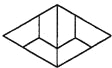
如图(a)所示,四边形ABCD是等腰梯形,AB∥DC、由4个这样的等腰梯形可以拼出图(b)所示的平行四边形.
(1)求四边形ABCD四个内角的度数;
(2)试探究四边形ABCD四条边之间存在的等量关系,并说明理由(思路提示:等腰梯形在同一底上的两个角相等,显然可以发现上底与腰相等);
(3)现有图(b)中的等腰梯形若干个,利用它们你能拼出一个菱形吗?若能,请你画出大致的示意图.(和你的同学交流)
分析:根据等腰梯形的三个上底上的底角正好构成周角,就可以求出上底角的度数,进而求出四个内角的度数.根据梯形腰和底边相等,就可以得到梯形四边之间的数量关系.
解答: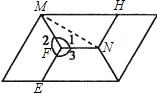 解:(1)如图,∠1=∠2=∠3,∠1+∠2+∠3=360°,即∠1=120°.
解:(1)如图,∠1=∠2=∠3,∠1+∠2+∠3=360°,即∠1=120°.
所以梯形的上底角均为120°,下底角为60°;
(2)由于EF既是梯形的腰,又是梯形的上底可知,梯形的腰等于上底.连接MN,
则∠FMN=∠FNM=
=30°,从而∠HMN=30°,∠HNM=90°.
所以NH=
MH.因此梯形的上底等于下底的一半,且等于腰长;
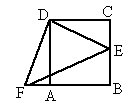
(3)能拼出菱形,如图:
梯形ABCD中,∠A=∠B=60°,则可作为正三角形的顶角,而∠D=∠C,则腰与上底可镶嵌在同一点周围能完成一个正三角形,故能拼出菱形.
 解:(1)如图,∠1=∠2=∠3,∠1+∠2+∠3=360°,即∠1=120°.
解:(1)如图,∠1=∠2=∠3,∠1+∠2+∠3=360°,即∠1=120°.所以梯形的上底角均为120°,下底角为60°;
(2)由于EF既是梯形的腰,又是梯形的上底可知,梯形的腰等于上底.连接MN,
则∠FMN=∠FNM=
| 180°-120° |
| 2 |
所以NH=
| 1 |
| 2 |

(3)能拼出菱形,如图:
梯形ABCD中,∠A=∠B=60°,则可作为正三角形的顶角,而∠D=∠C,则腰与上底可镶嵌在同一点周围能完成一个正三角形,故能拼出菱形.
点评:正确地观察图形之间存在的相等关系是解决本题的关键.

练习册系列答案
相关题目
 21、如图所示,某校在一块长40m,宽24m的土地上修一个矩形游泳池,并在四边各筑一条宽度相等的路,若游泳池的面积为720m2,求小路的宽.
21、如图所示,某校在一块长40m,宽24m的土地上修一个矩形游泳池,并在四边各筑一条宽度相等的路,若游泳池的面积为720m2,求小路的宽.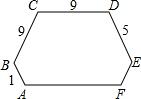 如图所示,一个六边形的六个内角都是120°,其中连续四边的长依次是1、9、9、5.求这个六边形的周长.
如图所示,一个六边形的六个内角都是120°,其中连续四边的长依次是1、9、9、5.求这个六边形的周长.