题目内容
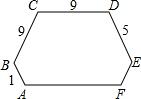 如图所示,一个六边形的六个内角都是120°,其中连续四边的长依次是1、9、9、5.求这个六边形的周长.
如图所示,一个六边形的六个内角都是120°,其中连续四边的长依次是1、9、9、5.求这个六边形的周长.分析:首先延长并反向延长AB,CD,EF,两两相交于点G、H、I,可得△GHI,△GBC是等边三角形,同理:△HAF,△DEI是等边三角形,即可求得AF与EF的长,继而求得答案.
解答: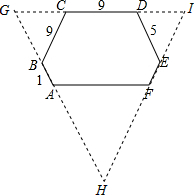 解:如图,延长并反向延长AB,CD,EF,两两相交于点G、H、I,
解:如图,延长并反向延长AB,CD,EF,两两相交于点G、H、I,
∵六边形ABCDEF的每个内角都是120°,
∴∠G=∠H=∠I=60°,∠GCB=∠GBC=60°,
∴△GHI,△GBC是等边三角形,
同理:△HAF,△DEI是等边三角形,
∴BG=GC=BC=9,DE=DI=EI=5,
∴GI=GC+CD+DI=9+9+5=23,
∴GH=GI=HI=23,
∴AH=GH-BG-AB=13,
∴AF=AH=FH=13,
∴EF=HI-EI-FH=5,
∴六边形ABCDEF的周长=AB+AF+EF+DE+CD+BC=1+13+5+5+9+9=42.
 解:如图,延长并反向延长AB,CD,EF,两两相交于点G、H、I,
解:如图,延长并反向延长AB,CD,EF,两两相交于点G、H、I,∵六边形ABCDEF的每个内角都是120°,
∴∠G=∠H=∠I=60°,∠GCB=∠GBC=60°,
∴△GHI,△GBC是等边三角形,
同理:△HAF,△DEI是等边三角形,
∴BG=GC=BC=9,DE=DI=EI=5,
∴GI=GC+CD+DI=9+9+5=23,
∴GH=GI=HI=23,
∴AH=GH-BG-AB=13,
∴AF=AH=FH=13,
∴EF=HI-EI-FH=5,
∴六边形ABCDEF的周长=AB+AF+EF+DE+CD+BC=1+13+5+5+9+9=42.
点评:本题考查了多边形的周长.解决本题的关键是构造等边三角形,根据等边三角形的三边相等的性质求解.

练习册系列答案
相关题目
 (2012•威海)向一个图案如图所示的正六边形靶子上随意抛一枚飞镖,则飞镖插在阴影区域的概率为( )
(2012•威海)向一个图案如图所示的正六边形靶子上随意抛一枚飞镖,则飞镖插在阴影区域的概率为( ) 如图所示,正六边形ABCDEF的边长是3cm,一个边长是1cm的小正方形沿着正六边形ABCDEF的边AB→BC→CD→DE→EF→FA→AB连续地翻转,那么这个小正方形第一次回到起始位置时,它的方向是( )
如图所示,正六边形ABCDEF的边长是3cm,一个边长是1cm的小正方形沿着正六边形ABCDEF的边AB→BC→CD→DE→EF→FA→AB连续地翻转,那么这个小正方形第一次回到起始位置时,它的方向是( )