题目内容
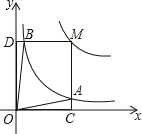
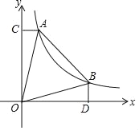
【题目】如图,A、B两点在反比例函数y=![]() (x>0)的图象上,其中k>0,AC⊥y轴于点C,BD⊥x轴于点D,且AC=1
(x>0)的图象上,其中k>0,AC⊥y轴于点C,BD⊥x轴于点D,且AC=1
(1)若k=2,则AO的长为 ,△BOD的面积为 ;
(2)若点B的横坐标为k,且k>1,当AO=AB时,求k的值.
【答案】(1)![]() ;1.(2)k=2+
;1.(2)k=2+![]() .
.
【解析】
(1)由AC和k的值可得出点A的坐标,利用勾股定理即可求出OA的长度,由点B在反比例函数图象上,利用反比例函数系数k的几何意义即可得出△BOD的面积;
(2)根据反比例函数图象上点的坐标特征可找出点A、B的坐标,利用两点间的距离公式即可求出AB、AO的长度,由AO=AB即可得出关于k的方程,解之即可求出k值,再根据k>1即可确定k值.
解:(1)∵AC=1,k=2,
∴点A(1,2),
∴OC=2,OA=![]() =
=![]() .
.
∵点B在反比例函数y=![]() (x>0)的图象上,
(x>0)的图象上,
∴S△BOD=![]() |k|=1.
|k|=1.
故答案为:![]() ;1.
;1.
(2)∵A,B两点在函数y=![]() (x>0)的图象上,
(x>0)的图象上,
∴A(1,k),B(k,1),
∴AO=![]() ,AB=
,AB=![]() .
.
∵AO=AB,
∴![]() =
=![]() ,
,
解得:k=2+![]() 或k=2﹣
或k=2﹣![]() .
.
∵k>1,
∴k=2+![]() .
.

练习册系列答案
相关题目