题目内容
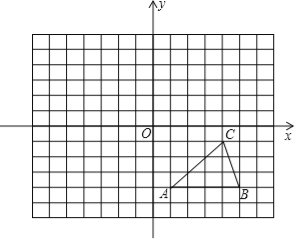
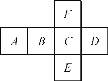
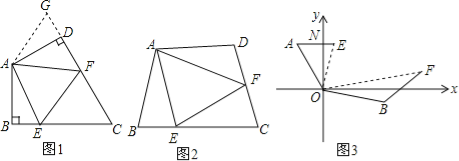
【题目】（13分）（1）如图1，在四边形ABCD中，AB=AD，∠BAD=120°，∠B=∠ADC=90°，E、F分别是BC、CD上的点，且∠EAF=60°，延长FD到点G，使DG=BE，连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得线段BE、EF、FD之间的数量关系为 ．
（2）如图2，在四边形ABCD中，AB=AD，∠B+∠D=180°，E、F分别是BC、CD上的点，且∠EAF=
∠BAD，线段BE、EF、FD之间存在什么数量关系，为什么？
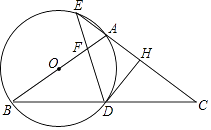
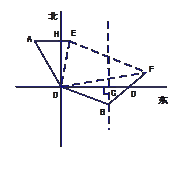
（3）如图3，点A在点O的北偏西30°处，点B在点O的南偏东70°处，且AO=BO，点A沿正东方向移动249米到达E处，点B沿北偏东50°方向移动334米到达点F处，从点O观测到E、F之间的夹角为70°，根据（2）的结论求E、F之间的距离．
【答案】（1）EF=BE+DF；（2）成立；（3）583m．
【解析】
试题（1）因为△AEF≌△AGF，所以EF=GF,又DG=BE，所以EF=BE+FD ；（2）类比（1）的作法，延长FD到点G，使DG=BE．连结AG，可证△ABE≌△ADG，△AEF≌△AGF，然后等量代换可得EF="GF=" BE+FD；（3）连结EF，由（2）的结论可得EF=AE+BF=249+334=583米.
试题解析：（1）EF=BE+FD 3分
（2）延长FD到点G，使DG=BE．连结AG，
∠B+∠ADF=180° ∴∠B=∠ADG 4分
又AB=AD BE=DG
∴△ABE≌△ADG， 5分
∴AE=AG ∠GAD=∠EAB
∵∠EAF=
∠BAD ∴∠EAF=∠GAF 6分 又AF=AF
∴△AEF≌△AGF，7分
∴EF="GF=" BE+FD 8分
（3）∠AOH=30° ∠BOD=20°
∠CBF=50°
∴∠OBF=120°
∴∠OBF+∠A=180° 10分
∠AOB=140° ∴∠EOF=∠AOB 12分
又AO=BO
∴根据（2）的结论可得EF=583米 13分
【题目】某教研机构为了解在校初中生阅读数学教科书的现状，随机抽取某校部分初中学生进行了调查．依据相关数据绘制成如图所示的不完整的统计图表，请根据图表中的信息解答下列问题：
某校初中生阅读数学教科书情况统计图表
类别 | 人数 | 占总人数比例 |
重视 | a | 0.3 |
一般 | 57 | 0.38 |
不重视 | b | c |
说不清楚 | 9 | 0.06 |
(1)求样本容量及表格中a，b，c的值，并补全统计图．
(2)若该校共有初中生2 300名，请估计该校“不重视阅读数学教科书”的初中生人数．
(3)①根据上面的统计结果，谈谈你对该校初中生阅读数学教科书的现状的看法及建议；
②如果要了解全省初中生阅读数学教科书的情况，你认为应该如何进行抽样？
