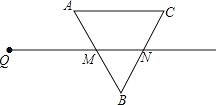题目内容
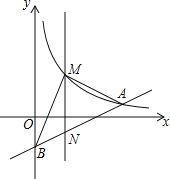
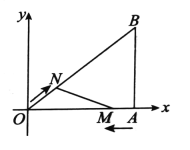
【题目】如图,在平面直角坐标系中,![]() 的直角顶点A在
的直角顶点A在![]() 轴上,OB=5,OA=4,动点M从点A出发,以每秒1个单位长度的速度,沿AO向终点O运动,同时点N从点O出发,以每秒2个单位长度的速度,沿OB向终点B移动,当两个动点运动了
轴上,OB=5,OA=4,动点M从点A出发,以每秒1个单位长度的速度,沿AO向终点O运动,同时点N从点O出发,以每秒2个单位长度的速度,沿OB向终点B移动,当两个动点运动了![]() 秒时,解答下列问题:
秒时,解答下列问题:
(1)若点B在反比例函数![]() 的图象上,求出该函数的解析式;
的图象上,求出该函数的解析式;
(2)在两个动点运动过程中,当![]() 为何值时,使得以O,M,N为顶点的三角形与
为何值时,使得以O,M,N为顶点的三角形与![]() 相似?
相似?
【答案】(1)![]() ;(2)当
;(2)当![]() 或
或![]() 秒时,使得以O,M,N为顶点的三角形与
秒时,使得以O,M,N为顶点的三角形与![]() 相似.
相似.
【解析】
(1)利用勾股定理求出AB,得出B的坐标,再把B的坐标代入解析式即可解答;
(2)在两个动点运动过程中,分两种情况:①若![]() ,得出
,得出![]() ,利用相似比的性质进行解答即可;②若
,利用相似比的性质进行解答即可;②若![]() ,得出
,得出![]() ,利用相似比的性质进行解答即可;
,利用相似比的性质进行解答即可;
(1)![]() 是直角三角形,且
是直角三角形,且![]() 轴于A,OA=4,OB=5
轴于A,OA=4,OB=5
![]()
![]()
将B(4,3)代入![]() 得
得![]()
![]()
(2)在两个动点运动过程中,分两种情况:
①若![]() ,如图所示,
,如图所示,
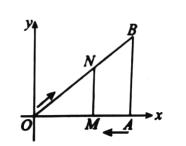
则MN∥AB,此时![]()
![]()
![]()
即:![]()
![]()
②若![]() ,如图所示,
,如图所示,
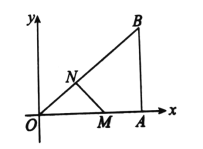
则![]() ,此时
,此时![]() ,
,
![]()
![]()
![]()
即:![]()
![]()
综上所述,当![]() 或
或![]() 秒时,使得以O,M,N为顶点的三角形与
秒时,使得以O,M,N为顶点的三角形与![]() 相似
相似

练习册系列答案
相关题目