题目内容
如图所示,在梯形ABCD中,AD∥BC,CE是∠BCD的平分线,且CE⊥AB,E为垂足,BE=2AE,若四边形AECD的面积为1,则梯形ABCD的面积为( )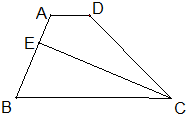


解:延长BA与CD,交于F,
∵AD∥BC,
∴△FAD∽△FBC,
∵CE是∠BCD的平分线,
∴∠BCE=∠FCE,
∵CE⊥AB,
∴∠BEC=∠FEC=90°,
∵EC=EC,
∴△BCE≌△FCE(ASA),
∴BE=EF,
∴BF=2BE,
∵BE=2AE,
∴EF=2AE,
∴AE=AF,
∴BF=4AE=4AF,
∴ ,
,
设S△FAD=x,
∴S△FBC=16x,
∴S△BCE=S△FEC=8x,
∴S四边形AECD=7x,
∵四边形AECD的面积为1,
∴7x=1,
∴x= ,
,
∴梯形ABCD的面积为:S△BCE+S四边形AECD=15x= .
.
故答案为: .
.

此题考查了梯形的性质,相似三角形的性质与判定,全等三角形的判定与性质等知识.此题综合性很强,解题的关键是方程思想与数形结合思想的应用.
∵AD∥BC,
∴△FAD∽△FBC,
∵CE是∠BCD的平分线,
∴∠BCE=∠FCE,
∵CE⊥AB,
∴∠BEC=∠FEC=90°,
∵EC=EC,
∴△BCE≌△FCE(ASA),
∴BE=EF,
∴BF=2BE,
∵BE=2AE,
∴EF=2AE,
∴AE=AF,
∴BF=4AE=4AF,
∴
 ,
,设S△FAD=x,
∴S△FBC=16x,
∴S△BCE=S△FEC=8x,
∴S四边形AECD=7x,
∵四边形AECD的面积为1,
∴7x=1,
∴x=
 ,
,∴梯形ABCD的面积为:S△BCE+S四边形AECD=15x=
 .
.故答案为:
 .
.
此题考查了梯形的性质,相似三角形的性质与判定,全等三角形的判定与性质等知识.此题综合性很强,解题的关键是方程思想与数形结合思想的应用.

练习册系列答案
相关题目
 ,AC=BC=2,M是边AC的中点,
,AC=BC=2,M是边AC的中点,






 面积是把菱形ABCD面积的一半,且BD=
面积是把菱形ABCD面积的一半,且BD= ,求则此菱形移动的距离.
,求则此菱形移动的距离.