题目内容
【题目】已知等边△ABC边长为8cm,点D是AC的中点,点E在射线BD上运动,以AE为边在AE右侧作等边△AEF,作射线CF交射线BD于点M,连接AM.
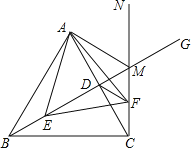
(1)当点E在线段BD(不包括端点B,D)上时,求证:BE=CF;
(2)求证:MA平分∠BMN;
(3)连接DF,点E在移动过程中,线段DF长的最小值等于 (直接写出结果)
【答案】(1)见解析;(2)见解析;(3)DF最小值为2cm.
【解析】
(1)欲证明BE=CF,只要证明△BAE≌△CAF(SAS)即可;
(2)首先证明∠BCM=90°,然后可得∠AMD=∠CMD=60°,求出∠AMN=60°即可;
(3)作DH⊥CN于H,根据点F的运动轨迹是射线CN可知,当点F与H重合时,DF的长最小,然后利用含30°直角三角形的性质求出DH即可.
(1)证明:∵△ABC,△AEF都是等边三角形,
∴AB=AC,AE=AF,∠BAC=∠EAF,
∴∠BAE=∠CAF,
∴△BAE≌△CAF(SAS),
∴BE=CF;
(2)证明:∵△ABC是等边三角形,AD=DC,
∴BD⊥AC,∠ACB=∠ABC=∠BAC=60°,
∴∠ABE=∠CBE=30°,MA=MC,
∵△BAE≌△CAF,
∴∠ABE=∠ACF=30°,
∴∠BCM=90°,
∴∠BMC=90°﹣30°=60°,
∵MA=MC,MB⊥AC,
∴∠AMD=∠CMD=60°,
∴∠AMN=60°,
∴∠AMN=∠AMD,
∴AM平分∠BMN.
(3)解:如图,作DH⊥CN于H.
∵∠BCN=90°,
∴点F的运动轨迹是射线CN,
根据垂线段最短可知,当点F与H重合时,DF的长最小,
∵CD=AD=4cm,∠DCH=30°,∠DHC=90°,
∴DH=![]() CD=2cm,
CD=2cm,
∴DF最小值为2cm.
故答案为2cm.


【题目】为了了解七年级学生体育测试成绩情况,现从中随机抽取部分学生的体育成绩统计如下,其中右侧扇形统计图中的圆心角α为36°,根据图表中提供的信息,回答下列问题:
体育成绩统计表 | ||
体育成绩(分) | 人数(人) | 百分比(%) |
26 | 8 | 16 |
27 | 12 | 24 |
28 | 15 | |
29 | n | |
30 | ||
(1)求样本容量及n的值;
(2)已知该校七年级共有500名学生,如果体育成绩达28分以上为优秀,请估计该校七年级学生体育成绩达到优秀的总人数.