题目内容
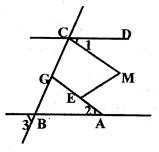
在等腰△ABC中,∠ACB=90°,且AC=1.过点C作直线l∥AB,P为直线l上一点,且AP=AB.则点P到BC所在直线的距离是
A.1
B.1或
C.1或
D. 或
或
A.1
B.1或

C.1或

D.
 或
或
D
分析:分点P与点A在BC同侧和异侧两种情况讨论:
①若点P与点A在BC同侧,如图,延长BC,作PD⊥BC,交点为D,延长CA,作PE⊥CA于点E,
∵CP∥AB,∴∠PCD=∠CBA=45°。∴四边形CDPE是正方形。
∴CD=DP=PE=EC。
在等腰Rt△ABC中,AC=BC=1,AB=AP,∴
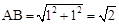 。∴AP=
。∴AP= 。
。在Rt△AEP中,
 ,即
,即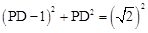 。解得,PD=
。解得,PD= 。
。②若点P与点A在BC异侧,如图,延长AC,做PD⊥BC交点为D,PE⊥AC,交点为E,

∵CP∥AB,∴∠PCD=∠CBA=45°。∴四边形CDPE是正方形。
∴CD=DP=PE=EC。
∵在等腰Rt△ABC中,AC=BC=1,AB=AP,
∴
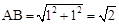 。∴AP=
。∴AP= 。
。∴在Rt△AEF中,
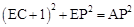 即
即
解得,DP=
 。
。故选D。

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目


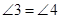




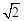 个单位长度的速度沿射线OD方向移动;同时点Q从点O出发,以每秒2个单位长度的速度沿x轴正方向移动.设移动时间为t秒.
个单位长度的速度沿射线OD方向移动;同时点Q从点O出发,以每秒2个单位长度的速度沿x轴正方向移动.设移动时间为t秒.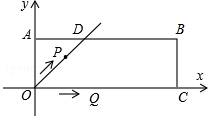
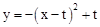 (t>0).问是否存在某一时刻t,将△PQB绕某点旋转180°后,三个对应顶点恰好都落在上述抛物线上?若存在,求出t的值;若不存在,请说明理由.
(t>0).问是否存在某一时刻t,将△PQB绕某点旋转180°后,三个对应顶点恰好都落在上述抛物线上?若存在,求出t的值;若不存在,请说明理由.