题目内容
【题目】一些完全相同的小正方形搭成一个几何体,这个几何体从正面和左面看所得的平面图形均如图所示,小正方体的块数可能有( )
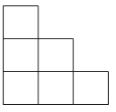
A. 7种 B. 8种 C. 9种 D. 10种
【答案】C
【解析】
从正面看得到的图形表现了几何体的长与高,从左面看得到的图形表现了几何体的宽和高,得到组合几何体的正方体的最多的个数和最少的个数,进而得到相应的可能情况总数即可.
解:由2个视图可得该组合几何体有3行,3列,所以最底层最多有9个正方体,最少有3个正方体;第二层最多有4个正方体,最少有2个正方体;第3层最多有1个正方体,最少有1个正方体,所以组合几何体最多有9+4+1=14个正方体,最少有3+2+1=6个正方体.
故正方体可能的个数在6和14之间,共有9种可能的情况,
故选C.

练习册系列答案
相关题目
【题目】某校要从甲、乙两名同学中挑选一人参加创新能力大赛,在最近的五次选拔测试中, 他俩的成绩分别如下表,请根据表中数据解答下列问题:
第 1 次 | 第 2 次 | 第 3 次 | 第 4 次 | 第 5 次 | 平均分 | 众数 | 中位数 | 方差 | |
甲 | 60 分 | 75 分 | 100 分 | 90 分 | 75 分 | 80 分 | 75 分 | 75 分 | 190 |
乙 | 70 分 | 90 分 | 100 分 | 80 分 | 80 分 | 80 分 | 80 分 |
(1)把表格补充完整:
(2)在这五次测试中,成绩比较稳定的同学是多少;若将 80 分以上(含 80 分) 的成绩视为优秀,则甲、乙两名同学在这五次测试中的优秀率分别是多少;
(3)历届比赛表明,成绩达到80分以上(含 80分)就很可能获奖,成绩达到 90分以上(含90分)就很可能获得一等奖,那么你认为选谁参加比赛比较合适?说明你的理由.