题目内容
在凸四边形ABCD中,AB=BC=BD,∠ABC=70°,则∠ADC等于
- A.145°
- B.150°
- C.155°
- D.160°
A
分析:根据等腰三角形性质求出∠C=∠BDC,∠A=∠BDA,根据多边形的内角和定理求出即可.
解答:∵AB=BC=BD,
∴∠C=∠BDC,∠A=∠BDA,
∵∠C+∠CDA+∠A+∠ABC=360°,
∴2(∠BDC+∠BDA)=360°-70°=290°,
∴∠BDC+∠BDA=145°,
即∠ADC=145°.
故选A.
点评:本题主要考查对等腰三角形性质,多边形的内角和定理等知识点的理解和掌握,能求出∠BDC+∠BDA的度数是解此题的关键.
分析:根据等腰三角形性质求出∠C=∠BDC,∠A=∠BDA,根据多边形的内角和定理求出即可.
解答:∵AB=BC=BD,
∴∠C=∠BDC,∠A=∠BDA,
∵∠C+∠CDA+∠A+∠ABC=360°,
∴2(∠BDC+∠BDA)=360°-70°=290°,
∴∠BDC+∠BDA=145°,
即∠ADC=145°.
故选A.
点评:本题主要考查对等腰三角形性质,多边形的内角和定理等知识点的理解和掌握,能求出∠BDC+∠BDA的度数是解此题的关键.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
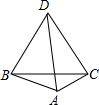 在凸四边形ABCD中,DA=DB=DC=BC,则这个四边形中最大角的度数是( )
在凸四边形ABCD中,DA=DB=DC=BC,则这个四边形中最大角的度数是( )| A、120° | B、135° | C、150° | D、165° |
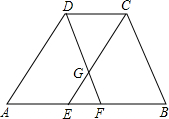 如图,在凸四边形ABCD中,AB∥CD,点E和F在边AB上,且CE∥AD,DF∥BC,DF与CE相交于点G,若△EFG的面积等于1,△CDG的面积等于2,则四边形ABCD的面积等于
如图,在凸四边形ABCD中,AB∥CD,点E和F在边AB上,且CE∥AD,DF∥BC,DF与CE相交于点G,若△EFG的面积等于1,△CDG的面积等于2,则四边形ABCD的面积等于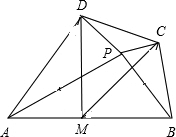 如图,在凸四边形ABCD中,M为边AB的中点,且MC=MD,分别过C,D两点,作边BC,AD的垂线,设两条垂线的交点为P.
如图,在凸四边形ABCD中,M为边AB的中点,且MC=MD,分别过C,D两点,作边BC,AD的垂线,设两条垂线的交点为P.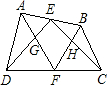 如图,在凸四边形ABCD中,E、F分别为边AB、CD的中点,AF、DE交于点G,BF、CE交于点H,四边形EGFH的面积为10.则△ADG与△BCH的面积和为( )
如图,在凸四边形ABCD中,E、F分别为边AB、CD的中点,AF、DE交于点G,BF、CE交于点H,四边形EGFH的面积为10.则△ADG与△BCH的面积和为( )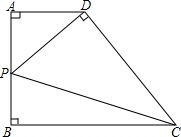 如图,在凸四边形ABCD中,AB的长为2,P是边AB的中点,若∠DAB=∠ABC=∠PDC=90°,则四边形ABCD的面积的最小值是( )
如图,在凸四边形ABCD中,AB的长为2,P是边AB的中点,若∠DAB=∠ABC=∠PDC=90°,则四边形ABCD的面积的最小值是( )