题目内容
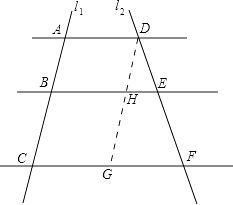
【题目】如图，已知AD∥BE∥CF，它们依次交直线l1、l2于点A、B、C和点D、E、F． 
（1）如果AB=6，BC=8，DF=21，求DE的长；
（2）如果DE：DF=2：5，AD=9，CF=14，求BE的长．
【答案】
（1）解：∵AD∥BE∥CF，
∴ 
，
∵AB=6，BC=8，DF=21，
∴ 
，
∴DE=9
（2）解：过点D作DG∥AC，交BE于点H，交CF于点G，
则CG=BH=AD=9，
∴GF=14﹣9=5，
∵HE∥GF，
∴ 
，
∵DE：DF=2：5，GF=5，
∴ 
，
∴HE=2，
∴BE=9+2=11．
【解析】（1）根据三条平行线截两条直线，所得的对应线段成比例可得 ，再由AB=6，BC=8，DF=21即可求出DE的长．（2）过点D作DG∥AC，交BE于点H，交CF于点G，运用比例关系求出HE及HB的长，然后即可得出BE的长．
【考点精析】本题主要考查了平行线分线段成比例的相关知识点，需要掌握三条平行线截两条直线，所得的对应线段成比例才能正确解答此题．
练习册系列答案
相关题目
