题目内容
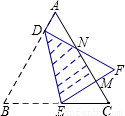
如图,将边长为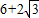 的等边△ABC折叠,折痕为DE,点B与点F重合,EF和DF分别交AC于点M、N,DF⊥AB,垂足为D,AD=2.设△DBE的面积为S,则重叠部分的面积为 .(用含S的式子表示)
的等边△ABC折叠,折痕为DE,点B与点F重合,EF和DF分别交AC于点M、N,DF⊥AB,垂足为D,AD=2.设△DBE的面积为S,则重叠部分的面积为 .(用含S的式子表示)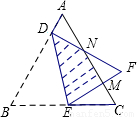
【答案】分析:由∠A=60°,AD=2,DF⊥AB,可求DN=2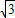 ,AN=4,由折叠的性质可知DF=DB=6+2
,AN=4,由折叠的性质可知DF=DB=6+2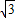 -AD=4+2
-AD=4+2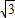 ,NF=DF-DN=4,则AN=NF,∠A=∠F=60°,∠AND=∠FNM,可证△ADN≌△FMN,根据S重叠部分=S△DEF-S△MNF=S△BDE-S△ADN求解.
,NF=DF-DN=4,则AN=NF,∠A=∠F=60°,∠AND=∠FNM,可证△ADN≌△FMN,根据S重叠部分=S△DEF-S△MNF=S△BDE-S△ADN求解.
解答:解:∵∠A=60°,AD=2,DF⊥AB,
∴在Rt△ADN中,DN=AD•tan60°=2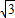 ,AN=
,AN=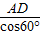 =4,
=4,
S△ADN= AD•DN=2
AD•DN=2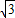 ,
,
由折叠的性质可知DF=DB=6+2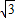 -AD=4+2
-AD=4+2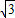 ,
,
∴NF=DF-DN=4,则AN=NF
又∠A=∠F=60°,∠AND=∠FNM,
∴△ADN≌△FMN,
∴S重叠部分=S△DEF-S△MNF=S△BDE-S△ADN=S-2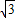 .
.
故答案为:S-2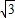 .
.
点评:本题考查了翻折变换(折叠问题),等边三角形的性质.关键是由已知推出特殊三角形,解直角三角形,由折叠的性质将线段进行转化.
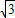 ,AN=4,由折叠的性质可知DF=DB=6+2
,AN=4,由折叠的性质可知DF=DB=6+2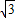 -AD=4+2
-AD=4+2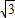 ,NF=DF-DN=4,则AN=NF,∠A=∠F=60°,∠AND=∠FNM,可证△ADN≌△FMN,根据S重叠部分=S△DEF-S△MNF=S△BDE-S△ADN求解.
,NF=DF-DN=4,则AN=NF,∠A=∠F=60°,∠AND=∠FNM,可证△ADN≌△FMN,根据S重叠部分=S△DEF-S△MNF=S△BDE-S△ADN求解.解答:解:∵∠A=60°,AD=2,DF⊥AB,
∴在Rt△ADN中,DN=AD•tan60°=2
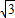 ,AN=
,AN=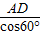 =4,
=4,S△ADN=
 AD•DN=2
AD•DN=2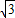 ,
,由折叠的性质可知DF=DB=6+2
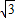 -AD=4+2
-AD=4+2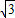 ,
,∴NF=DF-DN=4,则AN=NF
又∠A=∠F=60°,∠AND=∠FNM,
∴△ADN≌△FMN,
∴S重叠部分=S△DEF-S△MNF=S△BDE-S△ADN=S-2
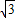 .
.故答案为:S-2
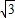 .
.点评:本题考查了翻折变换(折叠问题),等边三角形的性质.关键是由已知推出特殊三角形,解直角三角形,由折叠的性质将线段进行转化.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
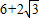 的等边△ABC折叠,折痕为DE,点B与点F重合,EF和DF分别交AC于点M、N,DF⊥AB,垂足为D,AD=2.设△DBE的面积为S,则重叠部分的面积为 .(用含S的式子表示)
的等边△ABC折叠,折痕为DE,点B与点F重合,EF和DF分别交AC于点M、N,DF⊥AB,垂足为D,AD=2.设△DBE的面积为S,则重叠部分的面积为 .(用含S的式子表示)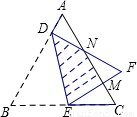
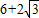 的等边△ABC折叠,折痕为DE,点B与点F重合,EF和DF分别交AC于点M、N,DF⊥AB,垂足为D,AD=2.设△DBE的面积为S,则重叠部分的面积为 .(用含S的式子表示)
的等边△ABC折叠,折痕为DE,点B与点F重合,EF和DF分别交AC于点M、N,DF⊥AB,垂足为D,AD=2.设△DBE的面积为S,则重叠部分的面积为 .(用含S的式子表示)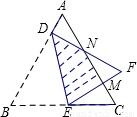
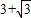 的等边△ABC折叠,折痕为DE,点B与点F重合,EF和DF分别交AC于点M、N,DF⊥AB,垂足为D,AD=1.设△DBE的面积为S,则重叠部分的面积为 .(用含S的式子表示)
的等边△ABC折叠,折痕为DE,点B与点F重合,EF和DF分别交AC于点M、N,DF⊥AB,垂足为D,AD=1.设△DBE的面积为S,则重叠部分的面积为 .(用含S的式子表示)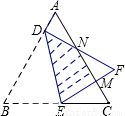
 的等边△ABC折叠,折痕为DE,点B与点F重合,EF和DF分别交AC于点M、N,DF⊥AB,垂足为D,AD=1.设△DBE的面积为S,则重叠部分的面积为 .(用含S的式子表示)
的等边△ABC折叠,折痕为DE,点B与点F重合,EF和DF分别交AC于点M、N,DF⊥AB,垂足为D,AD=1.设△DBE的面积为S,则重叠部分的面积为 .(用含S的式子表示)
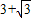 的等边△ABC折叠,折痕为DE,点B与点F重合,EF和DF分别交AC于点M、N,DF⊥AB,垂足为D,AD=1.设△DBE的面积为S,则重叠部分的面积为 .(用含S的式子表示)
的等边△ABC折叠,折痕为DE,点B与点F重合,EF和DF分别交AC于点M、N,DF⊥AB,垂足为D,AD=1.设△DBE的面积为S,则重叠部分的面积为 .(用含S的式子表示)