题目内容
对关于x的方程ax2+bx+c=0(a≠0).下列结论中:
①方程的解为 ;②若a+c=0,方程ax2+bx+c=0有两个不等的实数根;
;②若a+c=0,方程ax2+bx+c=0有两个不等的实数根;
③若方程ax2+bx+c=0有两个不等的实数根,则方程x2+bx+ac=0也一定有两个不等的实数根;④若二次三项式ax2+bx+c是完全平方式,则方程ax2+bx+c=0必有两相等实根;其中正确的结论是
- A.①③④
- B.①②④
- C.②③④
- D.①②③
C
分析:①根据根的判别式的情况进行判断;
②先整理出c=-a,然后利用根的判别式即可进行判断;
③根据两个方程的根的判别式进行判断;
④根据完全平方公式的结构,b=2 ,再求出根的判别式=0,即可进行判断.
,再求出根的判别式=0,即可进行判断.
解答:①若△=b2-4ac<0,则方程没有实数解,故本小题错误;
②∵a+c=0,
∴c=-a,
∴△=b2-4ac=b2-4a(-a)=b2+4a2,
∵b2≥0,4a2>0,
∴△>0,
∴方程ax2+bx+c=0有两个不等的实数根,故本小题正确;
③∵方程ax2+bx+c=0有两个不等的实数根,
∴△=b2-4ac>0,
方程x2+bx+ac=0的△=b2-4ac>0,
∴方程x2+bx+ac=0也一定有两个不等的实数根,故本小题正确;
④∵二次三项式ax2+bx+c是完全平方式,
∴b=2 ,
,
∴△=b2-4ac=b2-4× b2=0,
b2=0,
∴方程ax2+bx+c=0必有两相等实根,故本小题正确,
综上所述,正确的结论是②③④.
故选C.
点评:本题主要考查了根的判别式,一元二次方程根的情况与判别式△的关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.
求出各小题的△的正负情况是解题的关键.
分析:①根据根的判别式的情况进行判断;
②先整理出c=-a,然后利用根的判别式即可进行判断;
③根据两个方程的根的判别式进行判断;
④根据完全平方公式的结构,b=2
 ,再求出根的判别式=0,即可进行判断.
,再求出根的判别式=0,即可进行判断.解答:①若△=b2-4ac<0,则方程没有实数解,故本小题错误;
②∵a+c=0,
∴c=-a,
∴△=b2-4ac=b2-4a(-a)=b2+4a2,
∵b2≥0,4a2>0,
∴△>0,
∴方程ax2+bx+c=0有两个不等的实数根,故本小题正确;
③∵方程ax2+bx+c=0有两个不等的实数根,
∴△=b2-4ac>0,
方程x2+bx+ac=0的△=b2-4ac>0,
∴方程x2+bx+ac=0也一定有两个不等的实数根,故本小题正确;
④∵二次三项式ax2+bx+c是完全平方式,
∴b=2
 ,
,∴△=b2-4ac=b2-4×
 b2=0,
b2=0,∴方程ax2+bx+c=0必有两相等实根,故本小题正确,
综上所述,正确的结论是②③④.
故选C.
点评:本题主要考查了根的判别式,一元二次方程根的情况与判别式△的关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.
求出各小题的△的正负情况是解题的关键.

练习册系列答案
相关题目
 为a,b,c.若关于x的方程a(1-x2)+2bx+c(1+x2)=0有两个相等实数根,且a=b;
为a,b,c.若关于x的方程a(1-x2)+2bx+c(1+x2)=0有两个相等实数根,且a=b; 在△ABC中,a,b,c分别为∠A,∠B,∠C所对的边,我们称关于x的一元二次方程ax2+bx-c=0为“△ABC的☆方程”.根据规定解答下列问题:
在△ABC中,a,b,c分别为∠A,∠B,∠C所对的边,我们称关于x的一元二次方程ax2+bx-c=0为“△ABC的☆方程”.根据规定解答下列问题: 为a,b,c.若关于x的方程a(1-x2)+2bx+c(1+x2)=0有两个相等实数根,且a=b;
为a,b,c.若关于x的方程a(1-x2)+2bx+c(1+x2)=0有两个相等实数根,且a=b;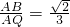 时求此抛物线的解析式;
时求此抛物线的解析式;