题目内容
 如图,M为⊙O内一点,且OM=5,若⊙O的半径为8,则过点M的弦长不可能为
如图,M为⊙O内一点,且OM=5,若⊙O的半径为8,则过点M的弦长不可能为
- A.16
- B.14
- C.12
- D.15
C
分析:过M的直径为16,即为最长的弦,最短的弦为垂直于直径OM的弦,利用垂径定理及勾股定理求出此时的弦长,即为最短的弦长,得到过M弦长的范围,即可得到正确的选项.
解答: 解:过M作直径CD,由半径为8,得到CD=16,
解:过M作直径CD,由半径为8,得到CD=16,
过M作AB⊥CD,交圆0于点A、B,连接OA,
∴M为AB的中点,即AM=BM,
在Rt△AOM中,OA=8,OM=5,
根据勾股定理得:AM=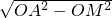 =
=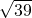 ,即AB=
,即AB=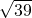 ,
,
∴过M弦长的范围为2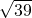 ≤x≤16,
≤x≤16,
则过M的弦长不可能为12.
故选C.
点评:此题考查了垂径定理,以及勾股定理,熟练掌握定理是解本题的关键.
分析:过M的直径为16,即为最长的弦,最短的弦为垂直于直径OM的弦,利用垂径定理及勾股定理求出此时的弦长,即为最短的弦长,得到过M弦长的范围,即可得到正确的选项.
解答:
 解:过M作直径CD,由半径为8,得到CD=16,
解:过M作直径CD,由半径为8,得到CD=16,过M作AB⊥CD,交圆0于点A、B,连接OA,
∴M为AB的中点,即AM=BM,
在Rt△AOM中,OA=8,OM=5,
根据勾股定理得:AM=
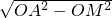 =
=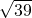 ,即AB=
,即AB=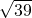 ,
,∴过M弦长的范围为2
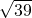 ≤x≤16,
≤x≤16,则过M的弦长不可能为12.
故选C.
点评:此题考查了垂径定理,以及勾股定理,熟练掌握定理是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
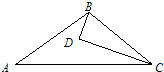 10、如图,D为△ABC内一点,CD平分∠ACB,BD⊥CD,∠A=∠ABD,若AC=5,BC=3,则BD的长为( )
10、如图,D为△ABC内一点,CD平分∠ACB,BD⊥CD,∠A=∠ABD,若AC=5,BC=3,则BD的长为( )
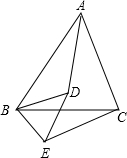 已知,如图,D为△ABC内一点连接BD、AD,以BC为边在△ABC外作∠CBE=∠ABD,∠BCE=∠BAD,BE、
已知,如图,D为△ABC内一点连接BD、AD,以BC为边在△ABC外作∠CBE=∠ABD,∠BCE=∠BAD,BE、 如图,M为⊙O内一点,且OM=5,若⊙O的半径为8,则过点M的弦长不可能为( )
如图,M为⊙O内一点,且OM=5,若⊙O的半径为8,则过点M的弦长不可能为( ) 如图,D为△ABC内一点,CD平分∠ACB,BD⊥CD,∠A=∠ABD,若AC=8,BC=5,则BD的长为
如图,D为△ABC内一点,CD平分∠ACB,BD⊥CD,∠A=∠ABD,若AC=8,BC=5,则BD的长为