ЬтФПФкШн
ЁОЬтФПЁПШчЭМ1ЃЌвбжЊ![]() ЪЧЕШБпШ§НЧаЮЃЌЕуEдкЯпЖЮABЩЯЃЌЕуDдкжБЯпBCЩЯЃЌЧв
ЪЧЕШБпШ§НЧаЮЃЌЕуEдкЯпЖЮABЩЯЃЌЕуDдкжБЯпBCЩЯЃЌЧв![]() ЃЌНЋ
ЃЌНЋ![]() ШЦЕуCЫГЪБеыа§зЊ
ШЦЕуCЫГЪБеыа§зЊ![]() жС
жС![]() ЃЌСЌНгEF.
ЃЌСЌНгEF.
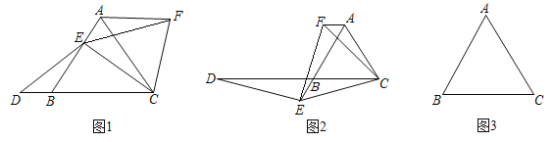
ЃЈ1ЃЉжЄУїЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌШчЙћЕуEдкЯпЖЮABЕФбгГЄЯпЩЯЃЌЦфЫћЬѕМўВЛБфЃЌЧыФуаДГіЯпЖЮABЁЂDBЁЂAFжЎМфЕФЪ§СПЙиЯЕЃЌВЂжЄУїФуЕФНсТлЃЛ
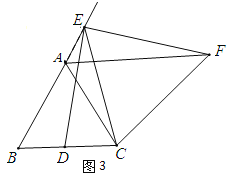
ЃЈ3ЃЉШчЙћЕуEдкЯпЖЮBAЕФбгГЄЯпЩЯЃЌЦфЫћЬѕМўВЛБфЃЌЧыдкЭМ3ЕФЛљДЁЩЯНЋЭМаЮВЙГфЭъећЃЌВЂаДГіABЁЂDBЁЂAFжЎМфЕФЪ§СПЙиЯЕЃЌВЛБижЄУї.
ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЛЃЈ2ЃЉABЃНBDЉAFЃЌжЄУїМћНтЮіЃЛЃЈ3ЃЉВЙГфЭМаЮМћНтЮіЃЌABЃЌDBЃЌAFжЎМфЕФЪ§СПЙиЯЕЪЧЃКAFЃНAB+BDЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЙ§ЕуEзїEGЁЮBCНЛACгкЕуGЃЌПЩЕУЁїAEGЮЊЕШБпШ§НЧаЮЃЌНјЖјПЩЕУBE=CGЃЌвзжЄЁЯBEDЃНЁЯGCEЃЌдйИљОнSASПЩжЄЁїBDEЁеЁїGECЃЌПЩЕУBDЃНEGЃНAEЃЌНјвЛВНМДЕУНсТлЃЛ
ЃЈ2ЃЉНсТлЃКABЃНBDЉAFЃЛШчЭМ2ЃЌбгГЄEFЁЂCAНЛгкЕуGЃЌЯШгЩа§зЊЕФаджЪжЄЕУЁїCEFЪЧЕШБпШ§НЧаЮЃЌНјЖјПЩЭЦЕУEDЃНEFЃЌШЛКѓРћгУШ§НЧаЮЕФЭтНЧаджЪПЩЭЦЕУЁЯFCGЃНЁЯFEAЃЌНјЖјПЩЕУЁЯDЃНЁЯFEAЃЌвзжЄЁЯDBEЃНЁЯFAEЃН60ЁуЃЌгкЪЧИљОнAASПЩжЄЁїEDBЁеЁїFEAЃЌПЩЕУBDЃНAEЃЌНјвЛВНИљОнЕШЯпЖЮДњЛЛМДПЩжЄЕУНсТлЃЛ
ЃЈ3ЃЉABЃЌDBЃЌAFжЎМфЕФЪ§СПЙиЯЕЪЧЃКAFЃНAB+BDЃЎШчЭМ3жаЃЌЯШИљОна§зЊЕФаджЪХаЖЯЁїCEFЪЧЕШБпШ§НЧаЮЃЌПЩЕУEFЃНECЃЌНјЖјПЩЕУEDЃНEFЃЌШЛКѓИљОнШ§НЧаЮЕФЭтНЧаджЪКЭНЧЖШжЎМфЕФЙиЯЕПЩЕУЁЯBDEЃНЁЯAEFЃЌвзжЄЁЯBЃНЁЯEAFЃН60ЁуЃЌгкЪЧИљОнAASПЩжЄЁїEDBЁеЁїFEAЃЌПЩЕУBDЃНAEЃЌEBЃНAFЃЌНјвЛВНМДПЩжЄЕУНсТл.
НтЃКЃЈ1ЃЉжЄУїЃКЁпЁїABCЪЧЕШБпШ§НЧаЮЃЌЁрAB=AC=BCЃЌЁЯABCЃНЁЯBCAЃН60ЁуЃЌ
ЁпЁїBCEШЦЕуCЫГЪБеыа§зЊ60ЁужСЁїACFЃЌЁрBEЃНAFЃЌ
ШчЭМ1ЃЌЙ§ЕуEзїEGЁЮBCНЛACгкЕуGЃЌдђЁїAEGЮЊЕШБпШ§НЧаЮЃЌЁрAE=AG=EGЃЌЁрBE=CGЃЌ
ЁпDEЃНCEЃЌЁрЁЯCDEЃНЁЯECDЃЌ
гжЁпЁЯCDE+ЁЯBEDЃНЁЯABCЃНЁЯACDЃНЁЯECD+ЁЯGCEЃЌ
ЁрЁЯBEDЃНЁЯGCEЃЌ
дкЁїBDEКЭЁїGECжаЃЌ
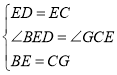 ЃЌ
ЃЌ
ЁрЁїBDEЁеЁїGECЃЈSASЃЉЃЌ
ЁрBDЃНEGЃНAEЃЌ
гжЁпAFЃНBEЃЌ
ЁрABЃНBE+AEЃНAF+BDЃЛ
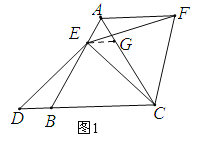
ЃЈ2ЃЉНсТлЃКABЃНBDЉAFЃЛ
РэгЩЃКШчЭМ2ЃЌбгГЄEFЁЂCAНЛгкЕуGЃЌ
ЁпЁїBCEШЦЕуCЫГЪБеыа§зЊ60ЁужСЁїACFЃЌ
ЁрЁЯECFЃН60ЁуЃЌBEЃНAFЃЌECЃНCFЃЌ
ЁрЁїCEFЪЧЕШБпШ§НЧаЮЃЌЁрEFЃНECЃЌ
гжЁпEDЃНECЃЌЁрEDЃНEFЃЌЁЯEFCЃНЁЯBACЃН60ЁуЃЌ
ЁпЁЯEFCЃНЁЯG+ЁЯFCGЃЌЁЯBACЃНЁЯG+ЁЯFEAЃЌ
ЁрЁЯFCGЃНЁЯFEAЃЌ
ЁпЁЯFCGЃНЁЯECDЃЌЁЯDЃНЁЯECDЃЌ
ЁрЁЯDЃНЁЯFEAЃЌ
гЩа§зЊЕФаджЪЕУЃКЁЯCBEЃНЁЯCAFЃН120ЁуЃЌгжЁпЁЯBAC=60ЁуЃЌ
ЁрЁЯDBEЃНЁЯFAEЃН60ЁуЃЌ
дкЁїEDBКЭЁїFEAжаЃЌ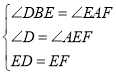 ЃЌ
ЃЌ
ЁрЁїEDBЁеЁїFEAЃЈAASЃЉЃЌ
ЁрBDЃНAEЃЌEBЃНAFЃЌ
ЁпAE=AB+BEЃЌ
ЁрBDЃНFA+ABЃЌ
МДABЃНBDЉAFЃЛ
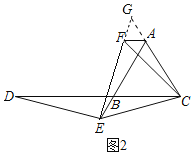
ЃЈ3ЃЉШчЭМ3жаЃЌABЃЌDBЃЌAFжЎМфЕФЪ§СПЙиЯЕЪЧЃКAFЃНAB+BDЃЎ
ЁпЁїBCEШЦЕуCЫГЪБеыа§зЊ60ЁужСЁїACFЃЌ
ЁрЁЯECFЃН60ЁуЃЌBEЃНAFЃЌECЃНCFЃЌЁрЁїCEFЪЧЕШБпШ§НЧаЮЃЌЁрEFЃНECЃЌ
гжЁпEDЃНECЃЌЁрEDЃНEFЃЌ
ЁпЁїABCЪЧЕШБпШ§НЧаЮЃЌ
ЁрЁЯBЃНЁЯBACЃН60ЁуЃЌ
гжЁпЁЯBЃНЁЯCAFЃЌЁрЁЯCAFЃН60ЁуЃЌ
ЁрЁЯEAFЃН180ЁуЉЁЯCAFЉЁЯBACЃН180ЁуЉ60ЁуЉ60ЁуЃН60ЁуЃЌ
ЁрЁЯBЃНЁЯEAFЃЛ
ЁпEDЃНECЃЌЁрЁЯECDЃНЁЯEDCЃЌ
ЁрЁЯBDEЃНЁЯECD+ЁЯDECЃНЁЯEDC+ЁЯDECЃЌ
гжЁпЁЯEDCЃНЁЯB+ЁЯBEDЃЌ
ЁрЁЯBDEЃНЁЯB+ЁЯBED+ЁЯDECЃН60Ёу+ЁЯBECЃЌ
ЁпЁЯAEFЃНЁЯCEF+ЁЯBECЃН60Ёу+ЁЯBECЃЌ
ЁрЁЯBDEЃНЁЯAEFЃЌ
дкЁїEDBКЭЁїFEAжаЃЌ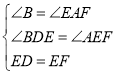 ЃЌ
ЃЌ
ЁрЁїEDBЁеЁїFEAЃЈAASЃЉЃЌ
ЁрBDЃНAEЃЌEBЃНAFЃЌ
ЁпBEЃНAB+AEЃЌ
ЁрAFЃНAB+BDЃЌ
МДABЃЌDBЃЌAFжЎМфЕФЪ§СПЙиЯЕЪЧЃКAFЃНAB+BDЃЎ

 ПЊаФСЗЯАПЮПЮСЗгыЕЅдЊМьВтЯЕСаД№АИ
ПЊаФСЗЯАПЮПЮСЗгыЕЅдЊМьВтЯЕСаД№АИ ПЊаФЪдОэЦкФЉГхДЬ100ЗжЯЕСаД№АИ
ПЊаФЪдОэЦкФЉГхДЬ100ЗжЯЕСаД№АИ




