题目内容
在坐标平面上,纵坐标与横坐标都是整数的点称为整点,试在二次函数y=| x2 |
| 10 |
| x |
| 10 |
| 9 |
| 5 |
分析:首先由y≤|x|,将y=
-
+
转化为
≤|x|,再从x大于等于0,以及小于0,分别分析得出符合要求的点.
| x2 |
| 10 |
| x |
| 10 |
| 9 |
| 5 |
| x2-x+18 |
| 10 |
解答:解:已知二次函数y=
-
+
,
即
≤|x|
有x2-x+18≤10|x|.
当x≥0时,有x2-11x+18≤0,
得2≤x≤9,代入二次函数,得合乎条件的4个整点:(2,2),(4,3),(7,6),(9,9);
当x<0时,
有x2+9x+18≤0,
得-6≤x≤-3,代入二次函数,得合乎条件的2个整点:
(-6,6),(-3,3).
∴这样的整点一共有6个:(-6,6),(-3,3),(2,2),(4,3),(7,6),(9,9).
| x2 |
| 10 |
| x |
| 10 |
| 9 |
| 5 |
即
| x2-x+18 |
| 10 |
有x2-x+18≤10|x|.
当x≥0时,有x2-11x+18≤0,
得2≤x≤9,代入二次函数,得合乎条件的4个整点:(2,2),(4,3),(7,6),(9,9);
当x<0时,
有x2+9x+18≤0,
得-6≤x≤-3,代入二次函数,得合乎条件的2个整点:
(-6,6),(-3,3).
∴这样的整点一共有6个:(-6,6),(-3,3),(2,2),(4,3),(7,6),(9,9).
点评:此题主要考查了取整函数的性质,得出
≤|x|,再进行分析是解决问题的关键.
| x2-x+18 |
| 10 |

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 -
-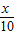 +
+ 的图象上找出满足y≤|x|的所有整点(x,y),并说明理由.
的图象上找出满足y≤|x|的所有整点(x,y),并说明理由.