题目内容
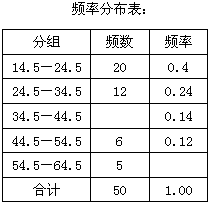
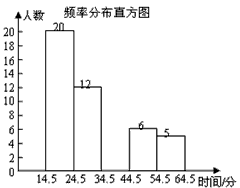
某中学为了解九年级300名学生的理化实验操作水平,从这300名学生中随机抽取30名学生进行测试,测试成绩5分以下(含5分)为不合格,6分至9分(含6分和9分)为良好,10分为优秀.下面是这30名学生的测试成绩表和相应的扇形统计图:
| 成绩 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 人数 | 2 | 4 | 6 | a | 7 | 2 | 2 | b |
(2)求出这30名学生测试成绩的平均数和众数;
(3)请估计该中学九年级300名学生中成绩为优秀的有多少人?
解:(1)b=30×10%=3(人),
良好的人数=30×50%=15(人),
∴a=15-7-2-2=4(人).
(2)平均数=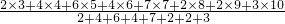 =6.3,
=6.3,
众数=7.
(3)该中学九年级300名学生中成绩为优秀人数=300×10%=30(人).
分析:(1)根据优秀人数占10%可求出b的值,根据良好的人数占的比例为50%,及7分、8分、9分的人数可得出a的值.
(2)根据平均数及众数的定义即可进行解答.
(3)频数=总数×频率,由此可得出300名学生中成绩为优秀的人数.
点评:本题考查了扇形统计图及图表信息的获取,要求学生能读懂扇形统计图,扇形统计图能够清楚地表示各部分所占的百分比.理解中位数的概念.能够根据样本估计总体.
良好的人数=30×50%=15(人),
∴a=15-7-2-2=4(人).
(2)平均数=
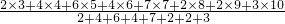 =6.3,
=6.3,众数=7.
(3)该中学九年级300名学生中成绩为优秀人数=300×10%=30(人).
分析:(1)根据优秀人数占10%可求出b的值,根据良好的人数占的比例为50%,及7分、8分、9分的人数可得出a的值.
(2)根据平均数及众数的定义即可进行解答.
(3)频数=总数×频率,由此可得出300名学生中成绩为优秀的人数.
点评:本题考查了扇形统计图及图表信息的获取,要求学生能读懂扇形统计图,扇形统计图能够清楚地表示各部分所占的百分比.理解中位数的概念.能够根据样本估计总体.

练习册系列答案
相关题目
我市某中学为了解九年级300名学生的理化实验操作水平,从中随机抽取30名学生进行测试.下表是这30名学生的测试成绩(分):
(1)请你设计一张统计表,能够清楚反映出各成绩的人数分布情况;
(2)求出这30名学生成绩的平均数、众数;
(3)如果测试成绩6分以上(包括6分)为合格,请估计300名学生中成绩合格的约有多少人?
| 4 | 5 | 7 | 6 | 3 | 7 | 9 | 4 | 5 | 7 |
| 7 | 3 | 7 | 5 | 6 | 8 | 7 | 5 | 6 | 8 |
| 6 | 7 | 4 | 10 | 5 | 6 | 7 | 3 | 9 | 4 |
(2)求出这30名学生成绩的平均数、众数;
(3)如果测试成绩6分以上(包括6分)为合格,请估计300名学生中成绩合格的约有多少人?
某中学为了解九年级300名学生的理化实验操作水平,从这300名学生中随机抽取30名学生进行测试,测试成绩5分以下(含5分)为不合格,6分至9分(含6分和9分)为良好,10分为优秀.下面是这30名学生的测试成绩表和相应的扇形统计图: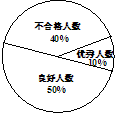
(1)求出测试成绩表中a和b的值;
(2)求出这30名学生测试成绩的平均数和众数;
(3)请估计该中学九年级300名学生中成绩为优秀的有多少人?

| 成绩 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 人数 | 2 | 4 | 6 | a | 7 | 2 | 2 | b |
(2)求出这30名学生测试成绩的平均数和众数;
(3)请估计该中学九年级300名学生中成绩为优秀的有多少人?