题目内容
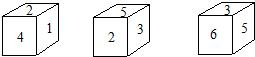
六个面分别标有1,1,x2+1,x,x+1,2x-1的小正方体的表面展开图如图所示,
(1)是否存在x,使得正方体相对的两面上数字相等,若存在,求出这样的x;若不存在,请说明理由;
(2)若六个面上的6个数之和为15,且x为正数,求出满足条件的x;
(3)掷这个正方体一次,记朝上一面的数为平面直角坐标系中某点的横坐标,朝下一面的数位该点的纵坐标,按照这样的规定,每抛一次该小正方体,就得到平面内一个点的坐标,求在(2)的条 件下抛一次正方体所得的点恰在直线y=2x-1上的概率.
件下抛一次正方体所得的点恰在直线y=2x-1上的概率.
(1)是否存在x,使得正方体相对的两面上数字相等,若存在,求出这样的x;若不存在,请说明理由;
(2)若六个面上的6个数之和为15,且x为正数,求出满足条件的x;
(3)掷这个正方体一次,记朝上一面的数为平面直角坐标系中某点的横坐标,朝下一面的数位该点的纵坐标,按照这样的规定,每抛一次该小正方体,就得到平面内一个点的坐标,求在(2)的条
 件下抛一次正方体所得的点恰在直线y=2x-1上的概率.
件下抛一次正方体所得的点恰在直线y=2x-1上的概率.分析:(1)x和2x-1相对,x2+1和x+1相对,从而列方程求解.
(2)6个面上的数字相加,根据和为15可求出解.
(3)看看有几对在y=2x-1上,从而求出概率.
(2)6个面上的数字相加,根据和为15可求出解.
(3)看看有几对在y=2x-1上,从而求出概率.
解答:解:(1)x=2x-1
x=1.
x2+1=x+1
x=1或x=0(舍去).
存在,x=1.
(2)x2+1+x+x+1+2x-1+1+1=15
x=2或x=-6(舍去).
因为x为正数,
所以x=2.
(3)相对面上的点为1,1;2,3;5,3.
在y=2x-1上的点为(1,1),(1,1),(3,2),(5,3).
(2,3),(3,5)不在上面.
故概率为:
.
x=1.
x2+1=x+1
x=1或x=0(舍去).
存在,x=1.
(2)x2+1+x+x+1+2x-1+1+1=15
x=2或x=-6(舍去).
因为x为正数,
所以x=2.
(3)相对面上的点为1,1;2,3;5,3.
在y=2x-1上的点为(1,1),(1,1),(3,2),(5,3).
(2,3),(3,5)不在上面.
故概率为:
| 2 |
| 3 |
点评:本题考查了一元二次方程的应用,一次函数图象上点的坐标特征,以及正方体相对两个面上的数字问题.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目