题目内容
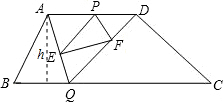
已知:在面积为7的梯形ABCD中,AD∥BC,AD=3,BC=4,P为边AD上不与A、D重合 的一动点,Q是边BC上的任意一点,连接AQ、DQ,过P作PE∥DQ交AQ于E,作PF∥AQ交DQ于F,则△PEF面积最大值是______.
的一动点,Q是边BC上的任意一点,连接AQ、DQ,过P作PE∥DQ交AQ于E,作PF∥AQ交DQ于F,则△PEF面积最大值是______.
 的一动点,Q是边BC上的任意一点,连接AQ、DQ,过P作PE∥DQ交AQ于E,作PF∥AQ交DQ于F,则△PEF面积最大值是______.
的一动点,Q是边BC上的任意一点,连接AQ、DQ,过P作PE∥DQ交AQ于E,作PF∥AQ交DQ于F,则△PEF面积最大值是______.设PD=x,S△PEF=y,S△AQD=z,梯形ABCD的高为h,
∵AD=3,BC=4,梯形ABCD面积为7,
∴
解得
∵PE∥DQ,
∴∠PEF=∠QFE,∠EPF=∠PFD,
又∵PF∥AQ,
∴∠PFD=∠EQF,
∴∠EPF=∠EQF,
∵EF=FE,
∴△PEF≌△QFE(AAS),
∵PE∥DQ,
∴△AEP∽△AQD,
同理,△DPF∽△DAQ,
∴
=(
)2,
=(
)2,
∵S△AQD=3,∴S△DPF=
x2,
S△APE=
(3-x)2,
∴S△PEF=(S△AQD-S△DPF-S△APE)÷2,
∴y=[3-
x2-
(3-x)2]×
=-
x2+x,
∵y最大值=
=
,即y最大值=
.
∴△PEF面积最大值是
.
∵AD=3,BC=4,梯形ABCD面积为7,
∴
|
解得
|
∵PE∥DQ,
∴∠PEF=∠QFE,∠EPF=∠PFD,
又∵PF∥AQ,
∴∠PFD=∠EQF,
∴∠EPF=∠EQF,
∵EF=FE,
∴△PEF≌△QFE(AAS),
∵PE∥DQ,
∴△AEP∽△AQD,
同理,△DPF∽△DAQ,
∴
| S△AEP |
| S△AQD |
| 3-x |
| 3 |
| S△DPF |
| S△DAQ |
| x |
| 3 |
∵S△AQD=3,∴S△DPF=
| 1 |
| 3 |
S△APE=
| 1 |
| 3 |
∴S△PEF=(S△AQD-S△DPF-S△APE)÷2,
∴y=[3-
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
∵y最大值=
| 0-12 | ||
4×(-
|
| 3 |
| 4 |
| 3 |
| 4 |
∴△PEF面积最大值是
| 3 |
| 4 |


练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目


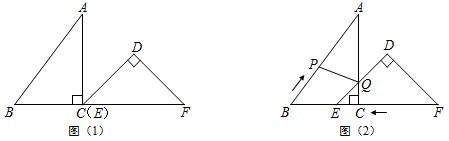

 与A,B重合),且保持DE
与A,B重合),且保持DE