题目内容
下列说法:①已知x、y互为相反数,a、b互为倒数,m的立方是它本身,则代数式4 (x+y)-ab+m3的值为-l或0;②若|a|=-a,则a是负数;③若a-b<0,ab<0,则a<0,b>0;④有一列按某种规律排列的数:2,-4,8,-16,32,-64,…,按此规律,写出第n项的那个数是(-2)n;其中正确的有
- A.O个
- B.1个
- C.2个
- D.3个
B
分析:①根据题意得到各个字母之间的关系.把它们代入所求的代数式求值;
②根据绝对值的性质可知非正数的绝对值等于它的相反数;
③根据异号两数相乘为负,可知a,b异号,再根据有理数的减法法则可知a<0,b>0;
④从排列的数:2,-4,8,-16,32,-64,…,可以知道每一项都是前一项的-2倍,第一项为2,知道为等比数列.
解答:①∵x、y互为相反数,a、b互为倒数,m的立方是它本身,
∴x+y=0,ab=1,m=0或±1,
当m=0时,原式=4×0-1+03=-1;
当m=-1时,原式=0-1+(-1)3=-2;
当m=1时,原式=0-1+13=0.
故代数式4 (x+y)-ab+m3的值为-l或-2或0.
故错误;
②∵|0|=-0,∴若|a|=-a,则a不一定是负数,故错误;
③∵ab<0,∴a,b异号,又∵a-b<0,∴a<0,b>0,故正确;
④第一项为2,第二项为(-2)×2=4,第三项为(-2)×(-4)=8,依此类推可以知道为等比数列,公比q=-2;
由此可以知道an=a1•qn-1,所以第n项为2×(-2)n-1化简为(-2)n+1,故错误.
故正确的有1个.
故选B.
点评:本题考查了代数式求值,绝对值的性质,等比数列,有理数的运算,综合性较强,有一定的难度.
分析:①根据题意得到各个字母之间的关系.把它们代入所求的代数式求值;
②根据绝对值的性质可知非正数的绝对值等于它的相反数;
③根据异号两数相乘为负,可知a,b异号,再根据有理数的减法法则可知a<0,b>0;
④从排列的数:2,-4,8,-16,32,-64,…,可以知道每一项都是前一项的-2倍,第一项为2,知道为等比数列.
解答:①∵x、y互为相反数,a、b互为倒数,m的立方是它本身,
∴x+y=0,ab=1,m=0或±1,
当m=0时,原式=4×0-1+03=-1;
当m=-1时,原式=0-1+(-1)3=-2;
当m=1时,原式=0-1+13=0.
故代数式4 (x+y)-ab+m3的值为-l或-2或0.
故错误;
②∵|0|=-0,∴若|a|=-a,则a不一定是负数,故错误;
③∵ab<0,∴a,b异号,又∵a-b<0,∴a<0,b>0,故正确;
④第一项为2,第二项为(-2)×2=4,第三项为(-2)×(-4)=8,依此类推可以知道为等比数列,公比q=-2;
由此可以知道an=a1•qn-1,所以第n项为2×(-2)n-1化简为(-2)n+1,故错误.
故正确的有1个.
故选B.
点评:本题考查了代数式求值,绝对值的性质,等比数列,有理数的运算,综合性较强,有一定的难度.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知∠1=17°18′,∠2=17.18°,∠3=17.3°,下列说法正确的是( )
| A、∠1=∠2 | B、∠1=∠3 | C、∠1=∠2 | D、∠2=∠3 |
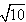 ; ②直角三角形的最大边长为
; ②直角三角形的最大边长为 ,最短边长为1,则另一边长为
,最短边长为1,则另一边长为 ; ③在
; ③在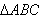 中,若
中,若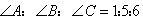 ,则
,则 为直角三角形; ④等腰三角形面积为12,底边上的高为4,则腰长为5。 正确的个数有
为直角三角形; ④等腰三角形面积为12,底边上的高为4,则腰长为5。 正确的个数有