题目内容
(2013•青岛)某商场要经营一种新上市的文具,进价为20元/件.试营销阶段发现:当销售单价是25元时,每天的销售量为250件;销售单价每上涨1元,每天的销售量就减少10件.
(1)写出商场销售这种文具,每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式;
(2)求销售单价为多少元时,该文具每天的销售利润最大;
(3)商场的营销部结合上述情况,提出了A、B两种营销方案:
方案A:该文具的销售单价高于进价且不超过30元;
方案B:每天销售量不少于10件,且每件文具的利润至少为25元
请比较哪种方案的最大利润更高,并说明理由.
(1)写出商场销售这种文具,每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式;
(2)求销售单价为多少元时,该文具每天的销售利润最大;
(3)商场的营销部结合上述情况,提出了A、B两种营销方案:
方案A:该文具的销售单价高于进价且不超过30元;
方案B:每天销售量不少于10件,且每件文具的利润至少为25元
请比较哪种方案的最大利润更高,并说明理由.
分析:(1)根据利润=(单价-进价)×销售量,列出函数关系式即可;
(2)根据(1)式列出的函数关系式,运用配方法求最大值;
(3)分别求出方案A、B中x的取值范围,然后分别求出A、B方案的最大利润,然后进行比较.
(2)根据(1)式列出的函数关系式,运用配方法求最大值;
(3)分别求出方案A、B中x的取值范围,然后分别求出A、B方案的最大利润,然后进行比较.
解答:解:(1)由题意得,销售量=250-10(x-25)=-10x+500,
则w=(x-20)(-10x+500)
=-10x2+700x-10000;
(2)w=-10x2+700x-10000=-10(x-35)2+2250.
∵-10<0,
∴函数图象开口向下,w有最大值,
当x=35时,wmax=2250,
故当单价为35元时,该文具每天的利润最大;
(3)A方案利润高.理由如下:
A方案中:20<x≤30,
故当x=30时,w有最大值,
此时wA=2000;
B方案中:
,
故x的取值范围为:45≤x≤49,
∵函数w=-10(x-35)2+2250,对称轴为直线x=35,
∴当x=45时,w有最大值,
此时wB=1250,
∵wA>wB,
∴A方案利润更高.
则w=(x-20)(-10x+500)
=-10x2+700x-10000;
(2)w=-10x2+700x-10000=-10(x-35)2+2250.
∵-10<0,
∴函数图象开口向下,w有最大值,
当x=35时,wmax=2250,
故当单价为35元时,该文具每天的利润最大;
(3)A方案利润高.理由如下:
A方案中:20<x≤30,
故当x=30时,w有最大值,
此时wA=2000;
B方案中:
|
故x的取值范围为:45≤x≤49,
∵函数w=-10(x-35)2+2250,对称轴为直线x=35,
∴当x=45时,w有最大值,
此时wB=1250,
∵wA>wB,
∴A方案利润更高.
点评:本题考查了二次函数的应用,难度较大,最大销售利润的问题常利函数的增减性来解答,我们首先要吃透题意,确定变量,建立函数模型,然后结合实际选择最优方案.其中要注意应该在自变量的取值范围内求最大值(或最小值),也就是说二次函数的最值不一定在x=-
时取得.
| b |
| 2a |

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
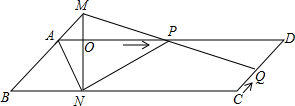 (2013•青岛)已知:如图,?ABCD中,AD=3cm,CD=1cm,∠B=45°,点P从点A出发,沿AD方向匀速运动,速度为3cm/s;点Q从点C出发,沿CD方向匀速运动,速度为1cm/s,连接并延长QP交BA的延长线于点M,过M作MN⊥BC,垂足是N,设运动时间为t(s)(0<t<1)
(2013•青岛)已知:如图,?ABCD中,AD=3cm,CD=1cm,∠B=45°,点P从点A出发,沿AD方向匀速运动,速度为3cm/s;点Q从点C出发,沿CD方向匀速运动,速度为1cm/s,连接并延长QP交BA的延长线于点M,过M作MN⊥BC,垂足是N,设运动时间为t(s)(0<t<1)