题目内容
九年级数学兴趣小组组织了以“等积变形”为主题的课题研究.
第一学习小组发现:如图(1),点A、点B在直线l1上,点C、点D在直线l2上,若l1∥l2,则S△ABC=S△ABD;反之亦成立.
第二学习小组发现:如图(2),点P是反比例函数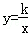 上任意一点,过点P作x轴、y轴的垂线,垂足为M、N,则矩形OMPN的面积为定值|k|.
上任意一点,过点P作x轴、y轴的垂线,垂足为M、N,则矩形OMPN的面积为定值|k|.
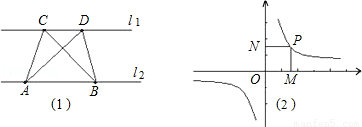
请利用上述结论解决下列问题:
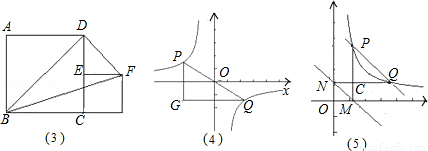
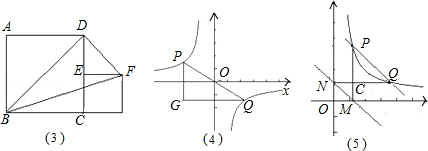
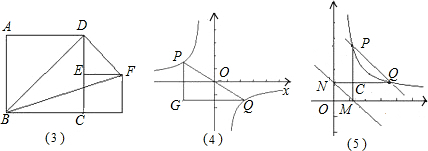
(1)如图(3),四边形ABCD、与四边形CEFG都是正方形点E在CD上,正方形ABCD边长为2,则S△BDF= 2 .
(2)如图(4),点P、Q在反比例函数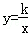 图象上,PQ过点O,过P作y轴的平行线交x轴于点H,过Q作x轴的平行线交PH于点G,若S△PQG=8,则S△POH= 2 ,k= ﹣4 .
图象上,PQ过点O,过P作y轴的平行线交x轴于点H,过Q作x轴的平行线交PH于点G,若S△PQG=8,则S△POH= 2 ,k= ﹣4 .
(3)如图(5)点P、Q是第一象限的点,且在反比例函数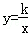 图象上,过点P作x轴垂线,过点Q作y轴垂线,垂足分别是M、N,试判断直线PQ与直线MN的位置关系,并说明理由.
图象上,过点P作x轴垂线,过点Q作y轴垂线,垂足分别是M、N,试判断直线PQ与直线MN的位置关系,并说明理由.
(1)2,(2)2,﹣4.(3)平行,理由见解析
【解析】
试题分析:(1)连接CF,根据正方形的性质可知,CF∥BD,△CBD与△FBD同底等高,故S△BDF=S△BDC,可求解;
(2)设P(x,y),则k=xy,根据P点所在象限及P、Q关于原点中心对称,得GQ=﹣2x,PG=2y,由已知,得S△PQG=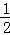 ×GQ×PG=8,可求S△POH及k的值;
×GQ×PG=8,可求S△POH及k的值;
(3)作PA⊥y轴,QB⊥x轴,垂足为A,B,连接PN,MQ,根据双曲线的性质可知,S矩形AOMP=S矩形BONQ=k,可得S矩形ANCP=S矩形BMCQ,则有S△NCP=S△MCQ,S△NPQ=S△MPQ,可证PQ∥MN.
解:(1)连接CF,
∵四边形ABCD与四边形CEFG都是正方形,
∴CF∥BD,△CBD与△FBD同底等高,
∴S△BDF=S△BDC=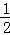 S正方形ABCD=2;
S正方形ABCD=2;
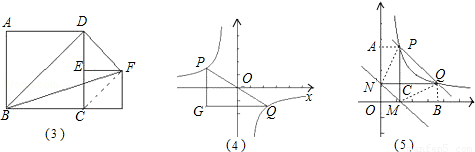
(2)设P(x,y),则k=xy,
根据题意,得GQ=﹣2x,PG=2y,
∴S△PQG= ×GQ×PG=8,即
×GQ×PG=8,即 ?(﹣2x)?2y=8,
?(﹣2x)?2y=8,
解得xy=﹣4,即k=﹣4,
S△POH= ×OH×PH=﹣
×OH×PH=﹣ xy=2;
xy=2;
(3)PQ∥MN.
理由:作PA⊥y轴,QB⊥x轴,垂足为A,B,连接PN,MQ,
根据双曲线的性质可知,S矩形AOMP=S矩形BONQ=k,
∴S矩形ANCP=S矩形BMCQ,可知S△NCP=S△MCQ,
∴S△NPQ=S△MPQ,
∴PQ∥MN.
故本题答案为:(1)2,(2)2,﹣4.
考点:反比例函数综合题;三角形的面积.
点评:本题通过反比例函数的知识,考查学生的猜想探究能力.解题时先直观地猜想,再按照从特殊到一般的方法去验证.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案

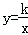 上任意一点,过点P作x轴、y轴的垂线,垂足为M、N,则矩形OMPN的面积为定值|k|.
上任意一点,过点P作x轴、y轴的垂线,垂足为M、N,则矩形OMPN的面积为定值|k|.
 上任意一点,过点P作x轴、y轴的垂线,垂足为M、N,则矩形OMPN的面积为定值|k|.
上任意一点,过点P作x轴、y轴的垂线,垂足为M、N,则矩形OMPN的面积为定值|k|.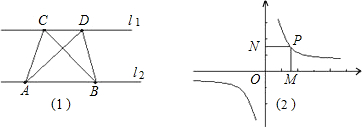
 上任意一点,过点P作x轴、y轴的垂线,垂足为M、N,则矩形OMPN的面积为定值|k|.
上任意一点,过点P作x轴、y轴的垂线,垂足为M、N,则矩形OMPN的面积为定值|k|.
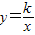 图象上,PQ过点O,过P作y轴的平行线交x轴于点H,过Q作x轴的平行线交PH于点G,若S△PQG=8,则S△POH=______,k=______.
图象上,PQ过点O,过P作y轴的平行线交x轴于点H,过Q作x轴的平行线交PH于点G,若S△PQG=8,则S△POH=______,k=______.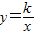 图象上,过点P作x轴垂线,过点Q作y轴垂线,垂足分别是M、N,试判断直线PQ与直线MN的位置关系,并说明理由.
图象上,过点P作x轴垂线,过点Q作y轴垂线,垂足分别是M、N,试判断直线PQ与直线MN的位置关系,并说明理由.