题目内容

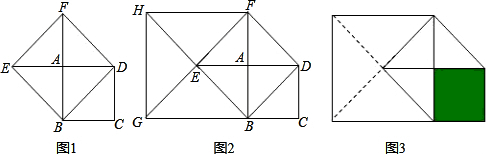
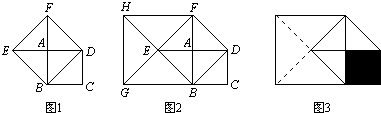
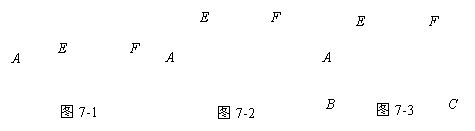
如图(1)所示，点O是∠EPF的平分线上的一点，以O为圆心的圆和角的两边分别交于点A、B和C、D．

求证：AB＝CD．

如果将∠EPF的顶点P看成是沿着PO这条直线运动的，那么

(1)当顶点P在⊙O上时(如图(2)所示)；是否能得到原来的结论？

(2)当顶点P在⊙O内部时(如图(3)所示)，是否能得到原来的结论？

答案：
解析：

要证明两弦AB=CD，根据本节所学的定理及推论，只要能证出圆心角、弧、弦心距三个量中的一个相等即可．由于已知PO是∠EPF的平分线，利用角平分线的性质可知点O到AB、CD的距离相等，即弦心距相等，于是可证明AB＝CD．

证明：作OM⊥AB，ON⊥CD，M、N为垂足

(1)(2)结论仍成立，证法同上．


练习册系列答案
相关题目
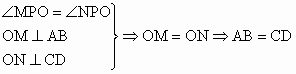
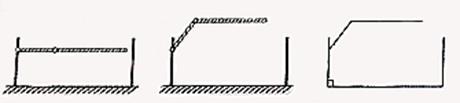
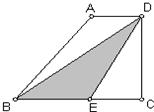21、如图，在直角梯形ABCD中，AD∥BC，CD⊥BC，E为BC边上的点．将直角梯形ABCD沿对角线BD折叠，使△ABD与△EBD重合（如图中阴影所示）．若∠A=130°，AB=4cm，求梯形ABCD的高CD的长．（结果精确到0.1cm）
（1）如图1，正方形ABCD的面积为2a，将正方形ABCD的对角线BD绕点B逆时针旋转90°至BE，以BD和BE为邻边作正方形BDFE，则此正方形BDFE的面积为
 
．（用含a的代数式表示）；
（2）如图2所示，再将正方形BDFE的对角线BF绕点B逆时针旋转90°至BG，以BF和BG为邻边作正方形BFHG，则此正方形BFHG的面积为
 
（用含a的代数式表示）；
（3）如果按着上述的过程作第三次旋转后，所得到的正方形的面积为
 
（用含a的代数式表示）；
（4）在一块边长为10米的正方形空地内种植上草坪（如图3阴影部分所示），由于这块正方形空地的左边和前边都有许多空地，所以，就在它的左边和前边（按着图2所示的过程）连续两次对这块草坪扩大种植面积，最后如图3所示的整个区域内都种上草坪，那么此时的草坪面积是多少平方米？
精英家教网
（1）如图1，正方形ABCD的面积为2a，将正方形ABCD的对角线BD绕点B按逆时针方向旋转90°至BE，以BD和BE为邻边作正方形BDFE，则正方形BDFE的面积为
 
（用含a的代数式表示）；
（2）如图2所示，再将正方形BDFE的对角线BF绕点B按逆时针方向旋转90°至BG，以BF和BG为邻边作正方形BFHG，则正方形BFHG的面积为
 
（用含a的代数式表示）；
（3）如果按着上述的过程作第2010次旋转后，所得到的正方形的面积为
 
（用含a的代数式表示）；
（4）在一块边长为10米的正方形空地内种上草坪（如图3阴影部分所示），由于这块正方形空地的左边和前边都有许多空地，所以，就在它的左边和前边（按着图2所示的过程）连续两次对这块草坪扩大种植面积，最后如图3所示的整个区域内都种上草坪，那么此时的草坪面积是多少平方米？
精英家教网
两张透明的三角形胶片完全重合摆放，如图1，所示△ABC和△DEF，将△DEF沿着公共边翻折180°，得到如图2，再把△DEF绕点B（E）按顺时针方向旋转，对应边AC与DF所在直线交于O
（1）当△DEF旋转至图3的位置即点B（E），F，A在同一条直线上，判断∠AFD与∠DCA是否相等，并予以证明；
（2）当△DEF旋转至B（E），F，A不共线时，画出其中一种图形，再判断（1）中结论是否还成立？并说明理由．

某地下车库出口处“两段式栏杆”如图7-1所示，点是栏杆转动的支点，点是栏杆两段的连接点．当车辆经过时，栏杆升起后的位置如图7-2所示，其示意图如图7-3所示，其中⊥，

∥，，米，求当车辆经过时，栏杆EF段距离地面的高度（即直线EF上任意一点到直线BC的距离）．

（结果精确到0.1米，栏杆宽度忽略不计参考数据：sin 37° ≈ 0.60，cos 37° ≈ 0.80，tan 37° ≈ 0.75．）

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网