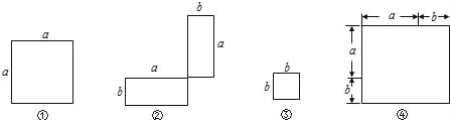
Ő‚ńŅńŕ»›
°ĺŐ‚ńŅ°Ņ»ÁÕľ1“—÷™ĺō–ő![]() £¨
£¨![]() £¨Ķ„
£¨Ķ„![]() ő™ĺō–ő÷––ń(
ő™ĺō–ő÷––ń(![]() ”Ž
”Ž![]() ĹĽĶ„)£¨Ō÷”–ŃĹ∂ĮĶ„
ĹĽĶ„)£¨Ō÷”–ŃĹ∂ĮĶ„![]() ∑÷Īū—ō◊Ň
∑÷Īū—ō◊Ň![]() ľį
ľį![]() Ķń∑ĹŌÚÕ¨ Ī≥Ų∑Ę‘»ňŔ‘ň∂Į£¨ňŔ∂»∂ľő™√Ņ√Ž“ĽłŲĶ•őĽ≥§∂»£¨ĶĪĶ„
Ķń∑ĹŌÚÕ¨ Ī≥Ų∑Ę‘»ňŔ‘ň∂Į£¨ňŔ∂»∂ľő™√Ņ√Ž“ĽłŲĶ•őĽ≥§∂»£¨ĶĪĶ„![]() ĶĹīÔ÷’Ķ„
ĶĹīÔ÷’Ķ„![]() ĪŃĹ∂ĮĶ„∂ľÕ£÷Ļ‘ň∂Į£¨Ń¨Ĺ”
ĪŃĹ∂ĮĶ„∂ľÕ£÷Ļ‘ň∂Į£¨Ń¨Ĺ”![]() £¨‘ŕ‘ň∂ĮĻż≥Ő÷–£¨…Ť‘ň∂Į Īľšő™
£¨‘ŕ‘ň∂ĮĻż≥Ő÷–£¨…Ť‘ň∂Į Īľšő™![]() £¨ŌŖ∂ő
£¨ŌŖ∂ő![]() ≥§∂»ő™
≥§∂»ő™![]() łŲĶ•őĽ≥§∂»£¨
łŲĶ•őĽ≥§∂»£¨![]() ”Ž
”Ž![]() ĶńļĮ żĻōŌĶ»ÁÕľ2
ĶńļĮ żĻōŌĶ»ÁÕľ2
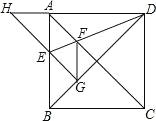
(1)![]() °° °°
°° °°![]() °° °°£ģ
°° °°£ģ
(2)![]() ő™∂ŗ…Ŕ Ī£¨ŌŖ∂ő
ő™∂ŗ…Ŕ Ī£¨ŌŖ∂ő![]() ĺ≠ĻżĶ„
ĺ≠ĻżĶ„![]() £Ņ≤Ę«“«ů≥Ųīň Ī
£Ņ≤Ę«“«ů≥Ųīň Ī![]() Ķń∂» ż£ģ
Ķń∂» ż£ģ
(3)‘ň∂ĮĻż≥Ő÷–£¨Ń¨Ĺ”![]() ļÕ
ļÕ![]() £¨«ůĶĪ
£¨«ůĶĪ![]() ő™÷ĪĹ« ĪĶń
ő™÷ĪĹ« ĪĶń![]() ÷Ķ£ģ
÷Ķ£ģ
°ĺīūįł°Ņ(1)5£¨10£Ľ(2)![]() £¨
£¨![]() £Ľ(3)ĶĪ
£Ľ(3)ĶĪ![]() ĽÚ
ĽÚ![]() Ī£¨
Ī£¨![]() ő™÷ĪĹ«.
ő™÷ĪĹ«.
°ĺĹ‚őŲ°Ņ
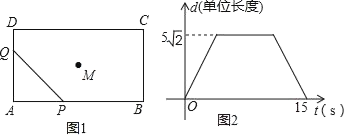
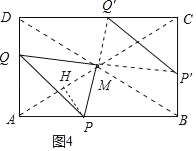
£®1£©ņŻ”√Õľ÷––ŇŌĘ£¨Ņ…÷™ĶĪĶ„QĶĹīÔĶ„D Ī£¨![]() £¨ľīŅ…Õ∆≥ŲAD=5£¨ĻŘ≤žÕľŌůŅ…÷™£ļĶ„P‘ŕŌŖ∂őAB…ŌĶń‘ň∂Į Īľšő™10s£¨”…īňľīŅ…«ů≥ŲABĶń≥§£Ľ
£¨ľīŅ…Õ∆≥ŲAD=5£¨ĻŘ≤žÕľŌůŅ…÷™£ļĶ„P‘ŕŌŖ∂őAB…ŌĶń‘ň∂Į Īľšő™10s£¨”…īňľīŅ…«ů≥ŲABĶń≥§£Ľ
£®2£©“◊÷™£ļĶĪDQ=PB Ī£¨PQĺ≠ĻżĶ„M£ģ”…īňĻĻĹ®∑Ĺ≥ŐľīŅ…Ĺ‚ĺŲő Ő‚£Ľ
£®3£©÷Ľ“™÷§√ų°ŌAMP=°ŌAMQ=45°„£¨…ŤPH=MH=a£¨‘ÚAH=2a£¨”…īňĻĻĹ®∑Ĺ≥ŐľīŅ…Ĺ‚ĺŲő Ő‚.
(1)”…Ő‚“‚£ļĶĪĶ„![]() ĶĹīÔĶ„
ĶĹīÔĶ„![]() Ī£¨
Ī£¨![]() £¨
£¨
![]() £¨
£¨
![]() £¨
£¨
![]() £¨
£¨
ĻŘ≤žÕľŌůŅ…÷™£ļĶ„![]() ‘ŕŌŖ∂ő
‘ŕŌŖ∂ő![]() …ŌĶń‘ň∂Į Īľšő™
…ŌĶń‘ň∂Į Īľšő™![]() £¨
£¨
![]() £¨
£¨
Ļ īūįłő™5£¨10£ģ
(2)»ÁÕľ3÷–£¨
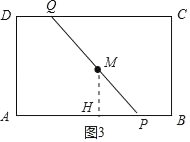
“◊÷™£ļĶĪ![]() Ī£¨
Ī£¨![]() ĺ≠ĻżĶ„
ĺ≠ĻżĶ„![]() £ģ
£ģ
‘Ú”–£ļ![]() £¨
£¨
![]() £¨
£¨
‘ŕ![]() ÷–£¨
÷–£¨![]() £¨
£¨
![]() £¨
£¨
![]() £ģ
£ģ
(3)»ÁÕľ4÷–£¨◊ų![]() ”ŕ
”ŕ![]() £ģ
£ģ
![]() £¨
£¨
![]() ňńĶ„Ļ≤‘≤£¨
ňńĶ„Ļ≤‘≤£¨
![]() £¨
£¨
![]() £¨
£¨
…Ť![]() £¨
£¨
![]() £¨
£¨
![]() £¨
£¨
![]() £¨
£¨
![]() £¨
£¨
![]() £¨
£¨
![]() £¨
£¨
![]() £¨īň Ī
£¨īň Ī![]() £¨
£¨
łýĺ›∂‘≥∆–‘Ņ…÷™£¨ĶĪ![]() Ī£¨
Ī£¨![]() £¨
£¨
![]() £¨
£¨
◊Ř…Ōňý Ų£¨ĶĪ![]() ĽÚ
ĽÚ![]() Ī£¨
Ī£¨![]() ő™÷ĪĹ«.
ő™÷ĪĹ«.

 ≥ŚīŐ100∑÷1ļŇĺŪŌĶŃ–īūįł
≥ŚīŐ100∑÷1ļŇĺŪŌĶŃ–īūįł ∆ŕń©ļ√≥…ľ®ŌĶŃ–īūįł
∆ŕń©ļ√≥…ľ®ŌĶŃ–īūįł°ĺŐ‚ńŅ°Ņń≥Ī®…Áő™ŃňŃňĹ‚ –√Ů°įĽŮ»°–¬őŇĶń◊Ó÷ų“™Õĺĺ∂°Ī£¨Ņ™’ĻŃň“Ľīő≥ť—ýĶų≤ť£¨łýĺ›Ķų≤ťĹŠĻŻĽś÷∆Ńň»ÁŌ¬»ż÷÷≤ĽÕÍ’ŻĶńÕ≥ľ∆ÕľĪŪ£ģ
◊ťĪū | ĽŮ»°–¬őŇĶń◊Ó÷ų“™Õĺĺ∂ | »ň ż |
| ĶÁń‘…ŌÕÝ | 280 |
| ÷Ľķ…ŌÕÝ |
|
| ĶÁ ” | 140 |
| Ī®÷Ĺ |
|
| ∆šňŻ | 80 |
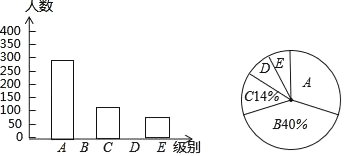
«Žłýĺ›ÕľĪŪ–ŇŌĘĹ‚īūŌ¬Ń–ő Ő‚£ļ
(1)Õ≥ľ∆ĪŪ÷–Ķń![]() °° °°£¨
°° °°£¨![]() °° °°£¨≤Ę«Ž≤Ļ»ęŐű–őÕ≥ľ∆Õľ£Ľ
°° °°£¨≤Ę«Ž≤Ļ»ęŐű–őÕ≥ľ∆Õľ£Ľ
(2)…»–őÕ≥ľ∆Õľ÷–°į![]() °Īňý∂‘”¶Ķń‘≤–ńĹ«Ķń∂» ż «°° °°£Ľ
°Īňý∂‘”¶Ķń‘≤–ńĹ«Ķń∂» ż «°° °°£Ľ
(3)»Űł√ –‘ľ”–100ÕÚ»ň£¨«Žń„Ļņľ∆∆š÷–Ĺę°įĶÁń‘…ŌÕÝ°ĪļÕ°į ÷Ľķ…ŌÕÝ°Ī◊ųő™°įĽŮ»°–¬őŇĶń◊Ó÷ų“™Õĺĺ∂°ĪĶń◊‹»ň ż£ģ