题目内容
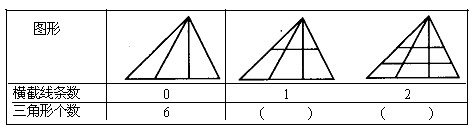
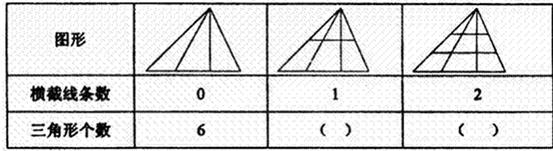
观察下表中三角形个数变化规律,填表并回答下面问题.
| 图形 | 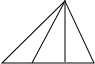 | 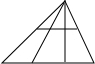 | 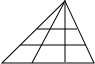 |
| 横截线条数 | 0 | 1 | 2 |
| 三角形个数 | 6 |
解:观察图形得到,1条横线有12个三角形,2条横线有18个三角形,
故答案为:12,18.
根据以上得到,设图中三角形的个数是102个有x条横线,则得:
102=6+6x,
解此方程得:x=16.
答:图中三角形的个数是102个,则图中应有16条横截线.
分析:观察所给图形得到,无横线(0条)是6个三角形,1条横线则是12个三角形,2条横线则是18个三角形,所以得到每有一条横线增加6个三角形,根据此规律设图中三角形的个数是102个有x条横线,得到关于x的方程,求出如果图中三角形的个数是102个,则图中应有多少条横截线.
点评:此题考查的知识点是图形数字变化类问题,解题的关键是观察总结规律,此题的规律是,有几条横截线就增加6的几倍的数的三角形.
故答案为:12,18.
根据以上得到,设图中三角形的个数是102个有x条横线,则得:
102=6+6x,
解此方程得:x=16.
答:图中三角形的个数是102个,则图中应有16条横截线.
分析:观察所给图形得到,无横线(0条)是6个三角形,1条横线则是12个三角形,2条横线则是18个三角形,所以得到每有一条横线增加6个三角形,根据此规律设图中三角形的个数是102个有x条横线,得到关于x的方程,求出如果图中三角形的个数是102个,则图中应有多少条横截线.
点评:此题考查的知识点是图形数字变化类问题,解题的关键是观察总结规律,此题的规律是,有几条横截线就增加6的几倍的数的三角形.

练习册系列答案
 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
观察下表中三角形个数变化规律,填表并回答下面问题.
| 图形 | 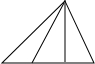 |  | 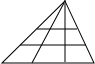 |
| 横截线条数 | 0 | 1 | 2 |
| 三角形个数 | 6 |
(1)当横截线条数为n条时应有______个三角形;
(2)如果图中三角形的个数是102个,则图中应有______条横截线.
观察下表中三角形个数变化规律,填表并回答下面问题.
问题:如果图中三角形的个数是102个,则图中应有 条横截线.
| 图形 | 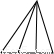 |  |  |
| 横截线条数 | 1 | 2 | |
| 三角形个数 | 6 |