题目内容
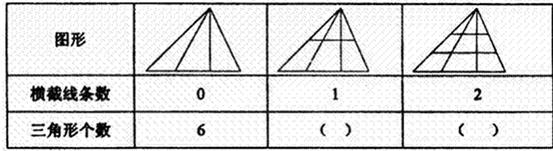
31、观察下表中三角形个数变化规律,填表并回答下面问题.
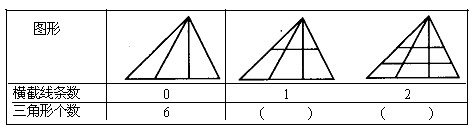
问题:
(1)当横截线条数为n条时应有
(2)如果图中三角形的个数是102个,则图中应有

问题:
(1)当横截线条数为n条时应有
6×(n+1)
个三角形;(2)如果图中三角形的个数是102个,则图中应有
16
条横截线.分析:根据三角形的概念和定义进行分析,注意不要遗漏.
解答:解:(1)没有横线的时候,只有6个三角形;
有一条横线的时候,有6×2个三角形;
有2条横线的时候,有6×3个三角形;
∴当横截线条数为n条时应有6×(n+1)个三角形.
(2)让6×(n+1)=102,
解得n=16.
有一条横线的时候,有6×2个三角形;
有2条横线的时候,有6×3个三角形;
∴当横截线条数为n条时应有6×(n+1)个三角形.
(2)让6×(n+1)=102,
解得n=16.
点评:解决本题的关键是观察简单图形,得到当横截线条数为n条时应有6×(n+1)个三角形.

练习册系列答案
相关题目
观察下表中三角形个数变化规律,填表并回答下面问题.
| 图形 | 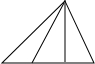 |  | 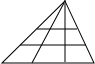 |
| 横截线条数 | 0 | 1 | 2 |
| 三角形个数 | 6 |
(1)当横截线条数为n条时应有______个三角形;
(2)如果图中三角形的个数是102个,则图中应有______条横截线.
观察下表中三角形个数变化规律,填表并回答下面问题.
问题:如果图中三角形的个数是102个,则图中应有 条横截线.
| 图形 | 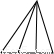 |  |  |
| 横截线条数 | 1 | 2 | |
| 三角形个数 | 6 |