题目内容
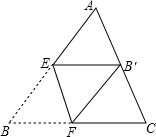将三角形纸片（△ABC）按如图所示的方式折叠，使点B落在边AC上，记为点B′，折痕为EF．若B′F∥AB，AB=AC=3，BC=4，那么BF的长度是分析：根据折叠的性质得到BF=FB′，设BF=x，则FC=4-x，FB′=x，而B′F∥AB，得到△CB′F∽△CAB，然后利用相似比得到关于x的方程，解方程即可．
解答：解：①∵折叠△ABC，使点B落在边AC上，记为点B′，折痕为EF．
∴BF=FB′，
而AB=AC=3，BC=4，
设BF=x，则FC=4-x，FB′=x，
∵B′F∥AB，
∴△CB′F∽△CAB，
∴
=
，
即
=
，
解得x=
．
②若FB=FC，即x=4-x，x=2．
故答案为：
或2．
∴BF=FB′，
而AB=AC=3，BC=4，
设BF=x，则FC=4-x，FB′=x，
∵B′F∥AB，
∴△CB′F∽△CAB，
∴
| FB′ |
| AB |
| CF |
| CB |
即
| x |
| 3 |
| 4-x |
| 4 |
解得x=
| 12 |
| 7 |
②若FB=FC，即x=4-x，x=2．
故答案为：
| 12 |
| 7 |
点评：本题考查了折叠的性质：折叠前后两图形全等，即对应角相等，对应线段相等．也考查了三角形相似的判定与性质．
练习册系列答案
相关题目
