题目内容
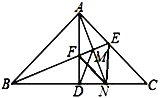
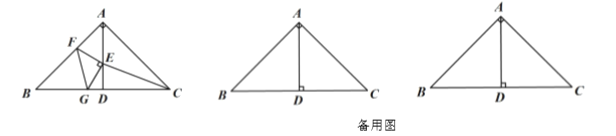
【题目】如图,![]() 是以
是以![]() 为斜边的等腰直角三角形,
为斜边的等腰直角三角形,![]() 为
为![]() 的中点,点
的中点,点![]() 、
、![]() 、
、![]() 分别为线段
分别为线段![]() ,
,![]() ,
,![]() 上的一点,
上的一点,![]() 以
以![]() 为直角顶点的等腰直角三角形,
为直角顶点的等腰直角三角形,![]() ,连结
,连结![]() .
.
(1)当![]() 与点
与点![]() 重合时,求
重合时,求![]() 的长.
的长.
(2)当![]() 时,求
时,求![]() 的面积.
的面积.
(3)①比较![]() 与
与![]() 的面积大小关系,并说明理由.
的面积大小关系,并说明理由.
②当![]() 的面积为6时,求
的面积为6时,求![]() 的长.
的长.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)①
;(3)①![]() ,理由见解析;②
,理由见解析;②![]()
【解析】
(1)依据等腰三角形的性质与勾股定理可以求得![]() ,依据三角形中等角对等边,可得
,依据三角形中等角对等边,可得![]() 是等腰三角形,依据等腰三角形三线合一的性质,可得
是等腰三角形,依据等腰三角形三线合一的性质,可得![]()
![]() ;
;
(2)过点![]() 作
作![]() 于点
于点![]() ,依据等角的余角相等,可用AAS证明
,依据等角的余角相等,可用AAS证明![]() ≌
≌![]() ,依据全等三角形的性质可得高为
,依据全等三角形的性质可得高为![]() ,再用
,再用![]() 求出底边
求出底边![]() ,最后用三角形面积公式可求
,最后用三角形面积公式可求![]() 的面积;
的面积;
(3)①设全等的![]() 和
和![]() 的对应边
的对应边![]() ,
,![]() ,则可用
,则可用![]() 、
、![]() 表示出两个三角形的面积,可依据三角形等角对等边的性质,得到
表示出两个三角形的面积,可依据三角形等角对等边的性质,得到![]() ,从而得到
,从而得到![]() 、
、![]() 间的关系
间的关系![]() ,将这个关系代入两个面积中,即可发现它们相等;
,将这个关系代入两个面积中,即可发现它们相等;
②当![]() 的面积为6时,可得到关于
的面积为6时,可得到关于![]() 、
、![]() 的等式,再结合
的等式,再结合![]() ,可解出
,可解出![]() 、
、![]() ,代入
,代入![]() 中即可.
中即可.
解:(1)∵![]() 是以
是以![]() 为斜边的等腰直角三角形,
为斜边的等腰直角三角形,![]() 为
为![]() 的中点,
的中点,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,同理
,同理![]() ,
,
如下图,当![]() 与点
与点![]() 重合时,
重合时,
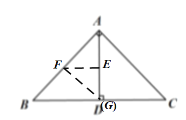
∵![]() 以
以![]() 为直角顶点的等腰直角三角形,
为直角顶点的等腰直角三角形,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ;
;
(2)如下图,过点![]() 作
作![]() 于点
于点![]() ,
,
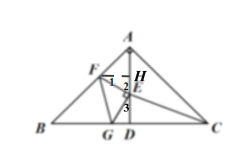
又∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
又∵![]() ,
,![]() ,
,
∴![]() ≌
≌![]() (AAS),
(AAS),
∴![]() ,
,
又∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() 的面积=
的面积=![]()
![]() .
.
(3)①![]() 与
与![]() 的面积相等,理由如下:
的面积相等,理由如下:
如下图,过点![]() 作
作![]() 于点
于点![]() ,则
,则![]() ,
,![]() ,
,

又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
由(2)知![]() ≌
≌![]() ,
,
∴设![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
又∵![]() ,
,![]() ,
,
∴![]() ,即
,即![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ;
;
②∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案
相关题目