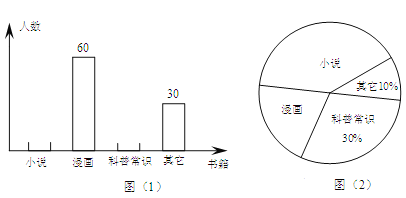
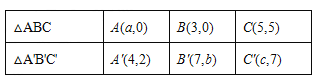
题目内容
【题目】如图所示,两个建筑物AB和CD的水平距离为30m,张明同学住在建筑物AB内10楼P室,他观测建筑物CD楼的顶部D处的仰角为30°,测得底部C处的俯角为45°,求建筑物CD的高度.(![]() 取1.73,结果保留整数.)
取1.73,结果保留整数.)
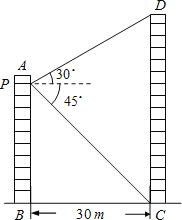
【答案】建筑物CD的高约为47m.
【解析】试题分析:过点P作PE⊥CD于E,则四边形BCEP是矩形,可得PE=BC=30m.在Rt△PDE中,由∠DPE=30°,PE=30m可计算出DE的长度为10![]() m,在Rt△PEC中,由∠EPC=45°,PE=30m可计算出CE的长度为30m,再对DE、CE求和即可.
m,在Rt△PEC中,由∠EPC=45°,PE=30m可计算出CE的长度为30m,再对DE、CE求和即可.
试题解析:
解:过点P作PE⊥CD于E,则四边形BCEP是矩形,
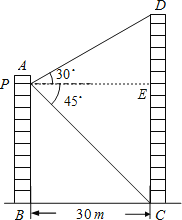
∴PE=BC=30m,
在Rt△PDE中,∵∠DPE=30°,PE=30 m,
∴DE=PE×tan30°=30×![]() =10
=10![]() m.
m.
在Rt△PEC中,∵∠EPC=45°,PE=30 m,
∴CE=PE×tan45°=30×1=30 m,
∴CD=DE+CE=30+10![]() =30+17.3≈47(m).
=30+17.3≈47(m).
答:建筑物CD的高约为47m.

 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案【题目】为了解某品牌轿车以![]() 匀速行驶的耗油情况,进行了试验:该轿车油箱加满后,以
匀速行驶的耗油情况,进行了试验:该轿车油箱加满后,以![]() 的速度匀速行驶,数据记录如下表:
的速度匀速行驶,数据记录如下表:
轿车行驶的路程 | 0 | 100 | 200 | 300 | … |
油箱剩余油量 | 50 | 41 | 32 | 23 | … |
(1)上表反映了哪两个变量之间的关系?自变量、因变量各是什么?
(2)油箱剩余油量![]() (升)与轿车行驶的路程
(升)与轿车行驶的路程![]() (千米)之间的关系式是什么?
(千米)之间的关系式是什么?
(3)若小明将油箱加满后,驾驶该轿车以![]() 的速度匀速从
的速度匀速从![]() 地驶往
地驶往![]() 地,到达
地,到达![]() 地时油箱剩余油量为5升,求两地之间的距离.
地时油箱剩余油量为5升,求两地之间的距离.
【题目】目前![]() 节能灯在城市已基本普及,为面向乡镇市场,苏宁电器分店决定用76000元购进室内用、室外用节能灯,已知这两种类型的节能灯进价、售价如下:
节能灯在城市已基本普及,为面向乡镇市场,苏宁电器分店决定用76000元购进室内用、室外用节能灯,已知这两种类型的节能灯进价、售价如下:
价格 类型 | 进价(元/盏) | 售价(元/盏) |
室内用节能灯 | 40 | 58 |
室外用节能灯 | 50 | 70 |
(1)若该分店共购进节能灯1700盏,问购进的室内用、室外用节能灯各多少盏?
(2)若该分店将进货全部售完后获利要不少于32000元,问至少需要购进多少盏室内用节能灯?
(3)挂职锻炼的大学生村官王祥自酬了4650元在该分店购买这两种类型的节能灯若干盏,分发给村民使用,其中室内用节能灯盏数不少于室内用节能灯盏数的2倍,问王祥最多购买室外用节能灯多少盏?